
分析 首先利用二项式定理求出a,然后根据定积分的几何意义求封闭图形的面积.
解答 解:因为在($\sqrt{x}$+$\frac{2}{\sqrt{x}}$)n的展开式中,第3项为常数项,所以${C}_{n}^{2}(\sqrt{x})^{n-2}(\frac{2}{\sqrt{x}})^{2}={C}_{n}^{2}(\sqrt{x})^{n-4}×4$为常数项,所以n=4,
又含x项的系数为a,所以${C}_{4}^{r}×{2}^{r}(\sqrt{x})^{4-2r}={C}_{4}^{r}{2}^{r}{x}^{2-r}$,令2-r=1,得r=1,所以a=8,
所以直线y=2x曲线y=x2所围成的封闭区域的面积为${∫}_{0}^{2}(2x-{x}^{2})dx$=(x${\;}^{2}-\frac{1}{3}{x}^{3}$)|${\;}_{0}^{2}$=$\frac{4}{3}$;
故答案为:$\frac{4}{3}$.
点评 本题考查了二项式定理的运用以及定积分的应用;正确求出a是解答的前提,利用定积分求封闭图形的面积是关键.


科目:高中数学 来源: 题型:解答题
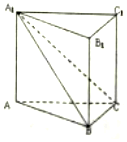 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面ABB1A1,且AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面ABB1A1,且AA1=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{6}}}{4}$ | D. | $\frac{{\sqrt{10}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | △PF1F2的内切圆圆心在直线$x=\frac{a}{2}$上 | B. | △PF1F2的内切圆圆心在直线x=b上 | ||
| C. | △PF1F2的内切圆圆心在直线OP上 | D. | △PF1F2的内切圆经过点(a,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
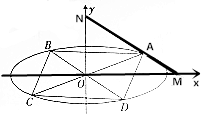 已知椭圆O:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点($\sqrt{3}$,-$\frac{1}{2}$),A(x0,y0)(x0y0≠0),其上顶点到直线$\sqrt{3}$x+y+3=0的距离为2,过点A的直线l与x,y轴的交点分别为M、N,且$\overrightarrow{AN}$=2$\overrightarrow{MA}$.
已知椭圆O:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点($\sqrt{3}$,-$\frac{1}{2}$),A(x0,y0)(x0y0≠0),其上顶点到直线$\sqrt{3}$x+y+3=0的距离为2,过点A的直线l与x,y轴的交点分别为M、N,且$\overrightarrow{AN}$=2$\overrightarrow{MA}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-$\frac{π}{6}$ | B. | x=$\frac{π}{12}$ | C. | x=-$\frac{π}{12}$ | D. | x=$\frac{π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com