
分析 (1)由已知得a1=2,an+1=an2+2an,由此利用递推思想能求出a3,a4的值.
(2)由$\frac{{lg({1+{a_{n+1}}})}}{{lg({1+{a_n}})}}=\frac{{lg({1+a_n^2+2{a_n}})}}{{lg({1+{a_n}})}}=\frac{{lg{{({1+{a_n}})}^2}}}{{lg({1+{a_n}})}}=2$,能数列{lg(1+an)}是等比数列,并能求出数列{an}的通项公式.
(3)推导出$\frac{1}{a_n}+\frac{1}{{{a_n}+2}}=\frac{2}{a_n}-\frac{2}{{{a_{n+1}}}},{b_n}=\frac{2}{a_n}-\frac{2}{{{a_{n+1}}}}$,由此利用裂项求和法能求出数列{bn}的前n项和Sn.
解答 解:(1)∵a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中n=1,2,3,….
∴${a_{n+1}}=a_n^2+2{a_n},{a_2}=a_1^2+2{a_1}=8,{a_3}=a_2^2+2{a_2}=80,{a_4}=a_3^2+2{a_3}=6560$.
证明:(2)∵$\frac{{lg({1+{a_{n+1}}})}}{{lg({1+{a_n}})}}=\frac{{lg({1+a_n^2+2{a_n}})}}{{lg({1+{a_n}})}}=\frac{{lg{{({1+{a_n}})}^2}}}{{lg({1+{a_n}})}}=2$,
∴{lg(1+an)}是首项为lg3,公比为2的等比数列,
∴$lg({1+{a_n}})=({lg3})×{2^{n-1}}=lg{3^{{2^{n-1}}}},1+{a_n}={3^{{2^{n-1}}}},{a_n}={3^{{2^{n-1}}}}-1$.
解:(3)${a_{n+1}}=a_n^2+2{a_n},\frac{1}{{{a_{n+1}}}}=\frac{1}{{a_n^2+2{a_n}}}=\frac{1}{2}({\frac{1}{a_n}-\frac{1}{{{a_n}+2}}}),\frac{1}{{{a_n}+2}}=\frac{1}{a_n}-\frac{2}{{{a_{n+1}}}}$,
∴$\frac{1}{a_n}+\frac{1}{{{a_n}+2}}=\frac{2}{a_n}-\frac{2}{{{a_{n+1}}}},{b_n}=\frac{2}{a_n}-\frac{2}{{{a_{n+1}}}}$,
∴${S_n}=\frac{2}{a_1}-\frac{2}{a_2}+\frac{2}{a_2}-\frac{2}{a_3}+\frac{2}{a_3}-\frac{2}{a_4}+…+\frac{2}{a_n}-\frac{2}{{{a_{n+1}}}}=\frac{2}{a_1}-\frac{2}{{{a_{n+1}}}}=1-\frac{2}{{{3^{2^n}}-1}}$.
点评 本题考查等比数列的证明,考查数列的通项公式和前n项和的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,一个直角走廊的宽分别为a米、b米,一铁棒欲通过该直角走廊,设铁棒与廊壁成θ角.求:
如图,一个直角走廊的宽分别为a米、b米,一铁棒欲通过该直角走廊,设铁棒与廊壁成θ角.求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示的正数数阵中,第一横行是公差为d的等差数列,各列均是公比为q等比数列,已知a1,1=1,a1,4=7,a4,1=$\frac{1}{8}$,则下列结论中不正确的是( )
如图所示的正数数阵中,第一横行是公差为d的等差数列,各列均是公比为q等比数列,已知a1,1=1,a1,4=7,a4,1=$\frac{1}{8}$,则下列结论中不正确的是( )| A. | d+2q=a1,2 | B. | a2,1+a2,3+a2,5+…+a2,21=$\frac{441}{2}$ | ||
| C. | 每一横行都是等差数列 | D. | ai,j=(2j-1)+21-i(i,j均为正整数) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
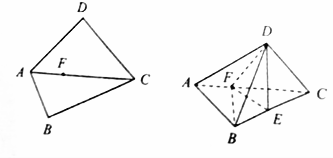 如图,平面四边形ABCD中,∠B=∠D=90°,AC=2AB=4$\sqrt{3}$,DA=DC,F是AC上一点,且AF=$\frac{1}{3}$AC.将该四边形沿AC折起,使点D在平面ABC的射影E恰在BC上,此时DE=2$\sqrt{2}$.
如图,平面四边形ABCD中,∠B=∠D=90°,AC=2AB=4$\sqrt{3}$,DA=DC,F是AC上一点,且AF=$\frac{1}{3}$AC.将该四边形沿AC折起,使点D在平面ABC的射影E恰在BC上,此时DE=2$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com