
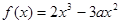 ,
,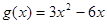 ,又函数
,又函数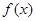 在
在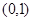 单调递减,而在
单调递减,而在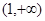 单调递增.
单调递增.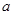 的值;
的值;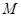 的最小值,使对
的最小值,使对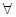
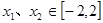 ,有
,有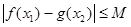 成立;
成立;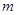 ,使得
,使得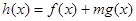 在
在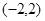 上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.
上既有最大值又有最小值?若存在,求出m的取值范围;若不存在,请说明理由.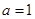 ,(2)满足条件的
,(2)满足条件的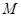 的最小值为52. (3)
的最小值为52. (3)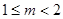
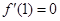 求出a的值.
求出a的值.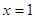 是函数
是函数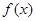 的一个极值点,即
的一个极值点,即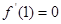 ,∴
,∴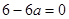 ,即
,即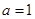 ,
,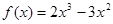 ,
,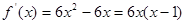 满足条件,∴
满足条件,∴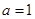 .………4分
.………4分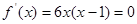 得,
得,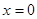 或
或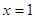 ,列表可得,
,列表可得, 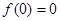 ,
,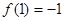 ,
,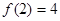 ,
,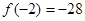 ,∴当
,∴当 时,
时,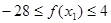 ;…………………6分
;…………………6分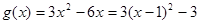 ,∴当
,∴当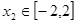 时,
时,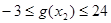 ;………8分
;………8分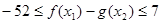 ,∴
,∴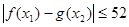 ;∴满足条件的
;∴满足条件的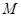 的最小值为52.…… 10分
的最小值为52.…… 10分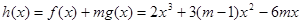
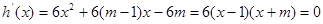 得
得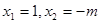 ;………12分
;………12分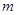 ,使得
,使得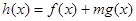 在
在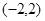 上既有最大值又有最小值,则必须
上既有最大值又有最小值,则必须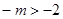 ,即
,即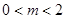 ,且满足
,且满足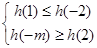 ,……………14分
,……………14分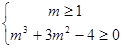 ,即
,即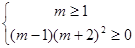 ∴
∴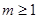 ∴
∴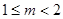 即为所求
即为所求

科目:高中数学 来源:不详 题型:单选题
| A.a=3,b=-3或a=―4,b=11; | B.a=-4,b=1或a=-4,b="11" ; |
| C.a=-1,b="5" ; | D.以上都不对 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 在区间[1,3]上为单调增函数,则实数a的取值范围是( )
在区间[1,3]上为单调增函数,则实数a的取值范围是( ) A.[ - ,+∞) ,+∞) | B.(-∞,-3] |
C.(-∞,-3]∪[- ,+∞) ,+∞) | D.[-  , ,  ] ] |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.2 | B.-2 | C.-4 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com