
分析 (1)利用组合数公式和排列数公式求解.
(2)利用组合数公式和排列数公式求解.
解答 解:(1)C104-C73A33
=$\frac{{A}_{10}^{4}}{{A}_{4}^{4}}$-$\frac{{A}_{7}^{3}}{{A}_{3}^{3}}$×${A}_{3}^{3}$
=$\frac{10×9×8×7}{4×3×2×1}$-7×6×5
=0.
(2)∵3A8x=4A9x-1.
∴3×$\frac{8!}{(8-x)!}$=4×$\frac{9}{(10-x)!}$,
∴3=$\frac{36}{(9-x)(10-x)}$,
(9-x)(10-x)=12,
解得x=6或x=13(舍),
∴x=6.
点评 本题考查组合数、排列数的求法,是基础题,解题时要认真审题,注意利用组合数公式和排列数公式的合理运用.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {2,3,4} | C. | {0,2,4} | D. | {0,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1或3 | B. | 1 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 4+2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
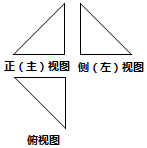 已知某几何体的正(主)视图,侧(左)视图和俯视图均为斜边长为$\sqrt{2}$的等腰直角三角形(如图),若该几何体的顶点都在同一球面上,则此球的表面积为( )
已知某几何体的正(主)视图,侧(左)视图和俯视图均为斜边长为$\sqrt{2}$的等腰直角三角形(如图),若该几何体的顶点都在同一球面上,则此球的表面积为( )| A. | 4π | B. | 3π | C. | 2π | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com