练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．已知点A（1，1），B（-2，2），则向量$\overrightarrow{OA}$与$\overrightarrow{BO}$的夹角为（　　） （其中O为坐标原点）
    A．30°B．90°C．60°D．120°

    分析 由已知点的坐标求出向量$\overrightarrow{OA}$与$\overrightarrow{BO}$的坐标，结合$\overrightarrow{OA}•\overrightarrow{BO}=0$得答案．

    解答 解：由A（1，1），B（-2，2），得$\overrightarrow{OA}=（1，1），\overrightarrow{BO}=（2，-2）$，
    ∴$\overrightarrow{OA}•\overrightarrow{BO}=0$，则向量$\overrightarrow{OA}$与$\overrightarrow{BO}$的夹角为90°．
    故选：B．

    点评 本题考查平面向量的数量积运算，考查向量垂直与夹角的关系，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    18．在梯形ABCD中，AD∥BC，∠ABC=90°，AB=a，AD=3a，且∠ADC=arcsin$\frac{{\sqrt{5}}}{5}$，PA⊥平面ABCD，PA=a，则二面角P-CD-A的大小为arctan$\frac{\sqrt{5}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．2015年5月1日世界博览会在意大利的米兰开幕，中国馆为了做好世界博览会期间的接待服务工作，从5名男大学生和3名女大学生中选出3人，参加博览会的志愿者服务活动．
    （Ⅰ）求选出的3人中至少1名女生的概率；
    （Ⅱ）设所选3人中女生人数为ξ，求ξ的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知向量$\overrightarrow{a}$=（$\sqrt{3}$cosωx，1），$\overrightarrow{b}$=（sinωx，cos2ωx-$\frac{1}{2}$）（ω＞0），函数f（x）=$\overrightarrow{a}•\overrightarrow{b}$，若函数f（x）的图象的一条对称轴与它相邻的一个对称中心的距离为$\frac{π}{4}$．
    （1）求f（x）的表达式；
    （2）将函数f（x）的图象向右平移$\frac{π}{4}$个单位，再将各点的横坐标缩短到原来的$\frac{1}{2}$（纵坐标不变），得到函数y=g（x）的图象，求函数g（x）在区间$[0，\frac{π}{4}]$上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

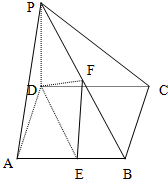    3．如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方体，PD=CD=2，E、F分别是AB、PB的中点
    （1）求证：EF⊥CD；
    （2）求DB与平面DEF所成角的大小；
    （3）在平面PAD内求一点G，使GF⊥平面PCB，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．过曲线C：y=ex上一点P0（0，1）作曲线C的切线l0交x轴于点Q1（x1，0），又过Q1作x轴的垂线交曲线C于点P1（x1，y1），然后再过P1（x1，y1）作曲线C的切线l1交x轴于点Q2（x2，0），又过Q2作x轴的垂线交曲线C于点P2（x2，y2），…，以此类推，过点Pn的切线ln与x轴相交于点
    Qn+1（xn+1，0），再过点Qn+1作x轴的垂线交曲线C于点Pn+1（xn+1，yn+1）（n∈N*）．
    （1）求x1、x2及数列{xn}的通项公式；
    （2）设曲线C与切线ln及直线Pn+1Qn+1所围成的图形面积为Sn，求Sn的表达式；
    （3）在满足（2）的条件下，若数列{Sn}的前n项和为Tn，求证：$\frac{{T}_{n+1}}{{T}_{n}}$＜$\frac{{x}_{n+1}}{{x}_{n}}$（n∈N+）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

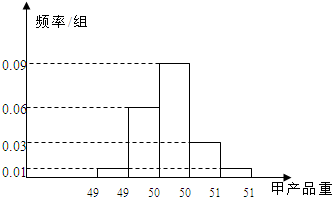    20．某食品厂为了检查甲、乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本．经统计，得到关于产品重量的样本频率分布直方图和样本频数分布表：
    乙流水线
    产品重量（单位：克）    		频数
    （490，495]6
    （495，500]8
    （500，505]14
    （505，510]8
    （510，515]4
    已知产品的重量合格标准为：重量值落在（495，510]内的产品为合格品；否则为不合格品．
    （1）从甲流水线样本的合格品中任意取2件，求重量值落在（505，510]的产品件数X的分布列；
    （2）从乙流水线中任取2件产品，试根据样本估计总体的思想，求其中合格品的件数Y的数学期望；
    （3）从甲、乙流水线中各取2件产品，用ξ表示“甲流水线合格品数与乙流水线合格品数的差的绝对值”，并用A表示事件“关于x的一元二次方程2x2+2ξx+ξ=0没有实数解”． 试根据样本估计总体的思想，求事件A的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知一个口袋中装有n个红球（n≥1且n∈N）和2个白球，从中有放回地连续摸三次，每次摸出两个球，若两个球颜色不同则为中奖，否则不中奖．
    （1）当n=3时，设三次摸球中（每次摸球后放回）中奖的次数为ξ，求的ξ分布列；
    （2）记三次摸球中（每次摸球后放回）恰有两次中奖的概率为P，当n取多少时，P最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知函数$f（x）=\left\{\begin{array}{l}{x^2}+2x-3，x≤0\\ lnx-a，x＞0\end{array}\right.（a∈R）$，若关于x的方程f（x）=k有三个不等的实根，则实数k的取值范围是（-4，-3）．

    查看答案和解析>>

    同步练习册答案