
 过曲线C:y=ex上一点P0(0,1)作曲线C的切线l0交x轴于点Q1(x1,0),又过Q1作x轴的垂线交曲线C于点P1(x1,y1),然后再过P1(x1,y1)作曲线C的切线l1交x轴于点Q2(x2,0),又过Q2作x轴的垂线交曲线C于点P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点
过曲线C:y=ex上一点P0(0,1)作曲线C的切线l0交x轴于点Q1(x1,0),又过Q1作x轴的垂线交曲线C于点P1(x1,y1),然后再过P1(x1,y1)作曲线C的切线l1交x轴于点Q2(x2,0),又过Q2作x轴的垂线交曲线C于点P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点分析 (1)先求出导函数进而求出切线的斜率,再把1,2代入就可求出求x1、x2的值.求出点Pn的切线ln的方程即可求出及数列{xn}的通项公式;
(2)直接利用定积分来求Sn的表达式即可;
(3)利用(2)的结论先求出数列{Sn}的前n项之和为Tn,再把所要证明的结论转化为用数学归纳法证明en+1>(e-1)n+e即可
解答 (1)解:由y′=ex,设直线ln的斜率为kn,则kn=e${\;}^{{x}_{n}}$.
∴直线l0的方程为y=x+1.令y=0,得x1=-1,
∴y1=e${\;}^{{x}_{1}}$=$\frac{1}{e}$,
∴P1(-1,$\frac{1}{e}$).
∴k1=e${\;}^{{x}_{1}}$=$\frac{1}{e}$.
∴直线l的方程为y-$\frac{1}{e}$=$\frac{1}{e}$(x+1).
令y=0,得x2=-2.
一般地,直线l的方程为y-e${\;}^{{x}_{n}}$=e${\;}^{{x}_{n}}$(x-xn),由于点Qn+1(xn+1,0)在直线l上,
∴xn+1-xn=-1.
∴数列{xn}是首项为-1,公差为-1的等差数列.
∴xn=-n.
(2)解:Sn=${∫}_{n+1}^{n}$exdx-$\frac{1}{2}$(xn-xn+1)yn=ex=${∫}_{n+1}^{n}$-$\frac{1}{2}$yn=(e-n-e-n-1)-$\frac{1}{2}$e-n=$\frac{e-2}{2e}$•$\frac{1}{{e}^{n}}$.
(3)证明:Tn=$\frac{e-2}{2e}$•($\frac{1}{{e}^{1}}$+$\frac{1}{{e}^{2}}$+…+$\frac{1}{{e}^{n}}$)=$\frac{e-2}{2e}$•$\frac{\frac{1}{e}[1-(\frac{1}{e})^{n}]}{1-\frac{1}{e}}$=$\frac{e-2}{2e(e-2)}$•(1-$\frac{1}{{e}^{n}}$),
∴$\frac{{T}_{n+1}}{{T}_{n}}$=$\frac{1-\frac{1}{{e}^{n+1}}}{1-\frac{1}{{e}^{n}}}$=1+$\frac{e-1}{{e}^{n+1}-e}$,$\frac{{x}_{n+1}}{{x}_{n}}$=$\frac{-(n+1)}{-n}$=1+$\frac{1}{n}$.
要证明$\frac{{T}_{n+1}}{{T}_{n}}$<$\frac{{x}_{n+1}}{{x}_{n}}$,只要证明$\frac{e-1}{{e}^{n+1}-e}$<$\frac{1}{n}$,即只要证明en+1>(e-1)n+e.
证法1:(数学归纳法)
①当n=1时,显然(e-1)2>0?e2>2e-1?e2>(e-1)+e成立;
②假设n=k时,ek+1>(e-1)k+e成立,则当n=k+1时,ek+2=e•ek+1>e[(e-1)k+e],
而e[(e-1)k+e]-[(e-1)(k+1)+e]=(e-1)2(k+1)>0,.
∴e[(e-1)k+e]>[(e-1)(k+1)+e].
∴ek+2>[(e-1)(k+1)+e.
这说明,n=k+1时,不等式也成立.
由①②知不等式$\frac{{T}_{n+1}}{{T}_{n}}$<$\frac{{x}_{n+1}}{{x}_{n}}$对一切n∈N+都成立.
证法2:en+1=[1+(e-1)]n+1=${C}_{n+1}^{0}$+${C}_{n+1}^{1}$(e-1)+…+${C}_{n+1}^{n+1}$(e-1)]n+1>${C}_{n+1}^{0}$+${C}_{n+1}^{1}$(e-1)=1+(n+1)(e-1)=(e-1)n+e.
∴不等式$\frac{{T}_{n+1}}{{T}_{n}}$<$\frac{{x}_{n+1}}{{x}_{n}}$对一切n∈N+都成立.
证法3:令f(x)=ex+1-(e-1)x-e,则f′(x)=ex+1-(e-1),
当x>0时,f′(x)=ex+1-(e-1)>e-(e-1)=1>0,
∴函数f(x)在(0,+∞)上单调递增.
∴当x>0时,f(x)>f(0)=0.
∵n∈N+,
∴f(n)>0,即en+1-(e-1)n-e>0.
∴en+1>(e-1)n+e.
∴不等式$\frac{{T}_{n+1}}{{T}_{n}}$<$\frac{{x}_{n+1}}{{x}_{n}}$对一切n∈N+都成立.
点评 主要考查导数、数列、不等式、定积分等知识,考查化归与转化的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 90° | C. | 60° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱O-ABCD锥中,底面ABCD四边长为4的菱形,∠ABC=60°,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
如图,在四棱O-ABCD锥中,底面ABCD四边长为4的菱形,∠ABC=60°,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
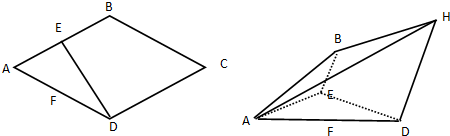
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com