
【题目】设函数![]() ,其中
,其中![]() 是实数.
是实数.
(l)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若
时,若![]() 为函数
为函数![]() 图像上一点,且直线
图像上一点,且直线![]() 与
与![]() 相切于点
相切于点![]() ,其中
,其中![]() 为坐标原点,求
为坐标原点,求![]() 的值;
的值;
(3) 设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,若
,若![]() 在定义域
在定义域![]() 内恒成立,则称函数
内恒成立,则称函数![]() 具有某种性质
具有某种性质![]() ,简称“
,简称“![]() 函数”.当
函数”.当![]() 时,试问函数
时,试问函数![]() 是否为“
是否为“![]() 函数”?若是,请求出此时切点
函数”?若是,请求出此时切点![]() 的横坐标;若不是,清说明理由.
的横坐标;若不是,清说明理由.
【答案】(1)增区间为![]() ,减区间为
,减区间为![]() ;(2)
;(2)![]() ;(3)是“
;(3)是“![]() 函数”,
函数”, ![]() .
.
【解析】试题分析:(1)求出![]() ,分别令
,分别令![]() 和
和![]() 可以得到函数的增区间和减区间.(2)由题设,曲线在
可以得到函数的增区间和减区间.(2)由题设,曲线在![]() 处的切线过原点,故
处的切线过原点,故![]()
![]() ,整理得到
,整理得到![]() ,根据函数
,根据函数![]() 为增函数以及
为增函数以及![]() 得到
得到![]() .(3)函数在
.(3)函数在![]() 处的切线方程为:
处的切线方程为: 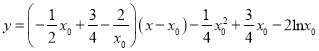 ,
,
构造函数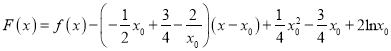
其导数为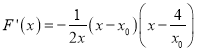 分别讨论
分别讨论![]() 和
和![]() 时
时![]() 的符号以及进一步讨论
的符号以及进一步讨论![]() 的单调性可知
的单调性可知![]() 在
在![]() 和
和![]() 上不是“
上不是“![]() 函数”,故
函数”,故![]() ,经检验符合.
,经检验符合.
解析:(1)由![]() ,得
,得![]() ,
, ![]() (
(![]() ),
),![]() , 由
, 由![]() 得:
得: ![]() ;由
;由![]() 得:
得: ![]() .所以
.所以![]() 的单调增区间为
的单调增区间为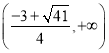 ,单调减区间为
,单调减区间为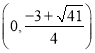 .
.
(2)由![]() ,得
,得![]() ,
, ![]() .
. ![]() , 所以切线的斜率
, 所以切线的斜率![]() .又切线
.又切线![]() 的斜率为
的斜率为![]() ,所以,
,所以, ![]()
![]() ,即
,即![]() ,设
,设![]() ,
, ![]() ,所以,函数
,所以,函数![]() 在(0,+∞)上为递增函数,且
在(0,+∞)上为递增函数,且![]() 是方程的一个解,即是唯一解,所以,.
是方程的一个解,即是唯一解,所以,.
(3)当![]() 时,由函数在其图象上一点处的切线方程为
时,由函数在其图象上一点处的切线方程为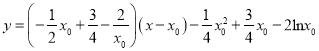 ,
,
令 
设![]() ,则
,则![]() .
.
且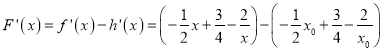
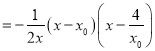
当![]() 时,
时, ![]() ,则在
,则在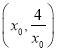 上有
上有![]() ,故在
,故在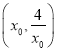 上
上![]() 单调递增,故当
单调递增,故当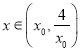 有
有![]() ,所以在
,所以在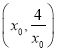 有
有![]() ;
;
当![]() 时,
时, ![]() ,则在
,则在 上有
上有![]() ,故在
,故在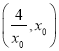 上
上![]() 单调递增,故当
单调递增,故当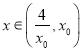 有
有![]() ,所以在
,所以在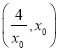 有
有![]() ;
;
因此,在![]() 上
上![]() 不是“
不是“![]() 函数”.
函数”.
当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减.
上单调递减.
所以, ![]() 时,
时, ![]() ,
, ![]() ;
;
![]() 时,
时, ![]() ,
, ![]() .因此,切点为点
.因此,切点为点![]() ,其横坐标为
,其横坐标为![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,求
的中点,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由已知,利用正弦定理可得![]() a2=
a2=![]() b2+
b2+![]() c2-2b,再利用余弦定理即可得出cosA,结合A的范围即可得解A的值.
c2-2b,再利用余弦定理即可得出cosA,结合A的范围即可得解A的值.
(2)△ABC中,先由正弦定理求得AC的值,再由余弦定理求得AB的值,△ABD中,由余弦定理求得BD的值.
试题解析:
(1)因为![]() asin A=(
asin A=(![]() b-c)sin B+(
b-c)sin B+(![]() c-b)·sin C,
c-b)·sin C,
由正弦定理得![]() a2=(
a2=(![]() b-c)b+(
b-c)b+(![]() c-b)c,
c-b)c,
整理得![]() a2=
a2=![]()
![]() c2-2bc,
c2-2bc,
由余弦定理得cos A=![]() =
=![]() =
=![]() ,
,
因为A∈(0,π),所以A=![]() .
.
(2)由cos B=![]() ,得sin B=
,得sin B=![]() =
=![]() =
=![]() ,
,
所以cos C=cos[π-(A+B)]=-cos(A+B)=-![]() =-
=-![]() ,
,
由正弦定理得b=![]() =
=![]() =2,
=2,
所以CD=![]() AC=1,
AC=1,
在△BCD中,由余弦定理得BD2=(![]() )2+12-2×1×
)2+12-2×1×![]() ×
×![]() =13,
=13,
所以BD=![]() .
.
【题型】解答题
【结束】
21
【题目】已知函数![]() 在
在![]() 处的切线经过点
处的切线经过点![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex(ax2﹣x﹣1)(a∈R).
(1)若函数f(x)在R上单调递减,求a的取值范围
(2)当a>0时,求f(|sinx|)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,角A,B,C的对边分别为a,b,c,R表示
中,角A,B,C的对边分别为a,b,c,R表示![]() 的外接圆半径.
的外接圆半径.
(Ⅰ)如图,在以O圆心、半径为2的![]() O中,BC和BA是
O中,BC和BA是![]() O的弦,其中
O的弦,其中![]() ,求弦AB的长;
,求弦AB的长;
(Ⅱ)在![]() 中,若
中,若![]() 是钝角,求证:
是钝角,求证:![]() ;
;
(Ⅲ)给定三个正实数a、b、R,其中![]() ,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的
,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的![]() 不存在、存在一个或存在两个(全等的三角形算作同一个)?在
不存在、存在一个或存在两个(全等的三角形算作同一个)?在![]() 存在的情况下,用a、b、R表示c.
存在的情况下,用a、b、R表示c.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项的和为Sn , 已知a1=1, ![]() =12.
=12.
(1)求{an}的通项公式an;
(2)bn= ![]() ,bn的前n项和Tn , 求证;Tn<
,bn的前n项和Tn , 求证;Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图像可以由y=cos2x的图像先纵坐标不变横坐标伸长到原来的2倍,再横坐标不变纵坐标伸长到原来的2倍,最后向右平移![]() 个单位而得到.
个单位而得到.
⑴求f(x)的解析式与最小正周期;
⑵求f(x)在x∈(0,π)上的值域与单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sin(
sin( ![]() +
+ ![]() )sin(
)sin( ![]() ﹣
﹣ ![]() )﹣sin(π+x),且函数y=g(x)的图象与函数y=f(x)的图象关于直线x=
)﹣sin(π+x),且函数y=g(x)的图象与函数y=f(x)的图象关于直线x= ![]() 对称.
对称.
(1)若存在x∈[0, ![]() ),使等式[g(x)]2﹣mg(x)+2=0成立,求实数m的最大值和最小值
),使等式[g(x)]2﹣mg(x)+2=0成立,求实数m的最大值和最小值
(2)若当x∈[0, ![]() ]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
]时不等式f(x)+ag(﹣x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :若关于
:若关于![]() 的方程
的方程![]() 无实数根,则
无实数根,则![]() ;命题
;命题![]() :若关于
:若关于![]() 的方程
的方程![]() 有两个不相等的正实数根,则
有两个不相等的正实数根,则![]() .
.
(1)写出命题![]() 的否命题,并判断命题
的否命题,并判断命题![]() 的真假;
的真假;
(2)判断命题“![]() 且
且![]() ”的真假,并说明理由.
”的真假,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com