
科目:高中数学 来源: 题型:
已知数列{an}的前n项和为Sn,且Sn=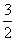 an-1(n∈N*).
an-1(n∈N*).
(1)求数列{an}的通项公式;
(2)在数列{bn}中,b1=5,bn+1=bn+an,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知曲线f(x)=xn+1(n∈N*)与直线x=1交于点P,设曲线y=f(x)在点P处的切线与x轴交点的横坐标为xn,则log2013x1+log2013x2+…+log2013x2012的值为( )
A.1 B.-1
C.2013 D.-2013
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列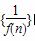 的前n项和为Sn,则S2014的值为( )
的前n项和为Sn,则S2014的值为( )
A.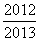 B.
B. C.
C.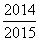 D.
D.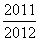
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=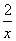 +lnx,则( )
+lnx,则( )
A.x= 为f(x)的极大值点
为f(x)的极大值点
B.x= 为f(x)的极小值点
为f(x)的极小值点
C.x=2为f(x)的极大值点
D.x=2为f(x)的极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ax2-1的图象在点A(1,f(1))处的切线l与直线8x-y+2=0平行,若数列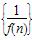 的前n项和为Sn,则S2010的值为( )
的前n项和为Sn,则S2010的值为( )
A.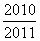 B.
B.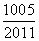
C. D.
D.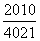
查看答案和解析>>
科目:高中数学 来源: 题型:
学习曲线是1936年美国康乃尔大学T.P.Wright博士在飞机制造过程中,通过对大量有关资料、案例的观察、分析、研究,首次发现并提出来的.已知某类学习任务的学习曲线为:f(t)=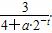 ·100%(其中f(t)为掌握该任务的程度,t为学习时间),且这类学习任务中的某项任务满足f(2)=60%.
·100%(其中f(t)为掌握该任务的程度,t为学习时间),且这类学习任务中的某项任务满足f(2)=60%.
(1)求f(t)的表达式,计算f(0)并说明f(0)的含义;
(2)已知2x>xln2对任意x>0恒成立,现定义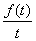 为该类学习任务在t时刻的学习效率指数,研究表明,当学习时间t∈(1,2)时,学习效率最佳,当学习效率最佳时,求学习效率指数相应的取值范围.
为该类学习任务在t时刻的学习效率指数,研究表明,当学习时间t∈(1,2)时,学习效率最佳,当学习效率最佳时,求学习效率指数相应的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com