
����Ŀ������Ϊ��ǿ����Ļ���������ʶ������ȫ��������������־Ը�ߣ��ִӷ���������־Ը���������ȡ100����������飺��1��![]() ����2��
����2��![]() ����3��
����3��![]() ����4��
����4��![]() ����5��
����5��![]() ���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��

��1���ֱ����3��4��5���Ƶ�ʣ�
��2�����ӵ�3��4��5�����÷ֲ�����ķ�����ȡ6��־Ը�߲μӹ㳡�������Ӧ�ӵ�3��4��5�����ȡ������־Ը�ߣ�
��3���ڣ�2���������£����о�������6��־Ը���������ȡ2��־Ը�߽����������飬���4��������һ��־Ը�߱����еĸ��ʣ�
���𰸡�(1) ��3���Ƶ��Ϊ0��3����4���Ƶ��Ϊ0��2����5���Ƶ��Ϊ0��1;(2) �ӵ�3��4��5���зֱ��ȡ3�ˣ�2�ˣ�1��;(3) ��4��������һ��־Ը�߱����еĸ���Ϊ![]() .
.
�������������������1����ͼ��֪��Ƶ��= ![]() ���=5y,����ø���Ƶ�ʡ���2���ɣ�1����֪��3��4��5���Ƶ�ʷֱ�Ϊ��0.3,0.2,0.1�����Ը�������Ϊ30,20,10,���ֲ������3:2:1��ȡ�����Ե�3��4��5��ֱ��3�ˣ�2�ˣ�1�ˡ���3���ɣ�2��֪��3��4��5���зֱ��ȡ3�ˣ�2�ˣ�1�ˣ��ǵ�3���3��־Ը��ΪA1��A2��A3����4���2��־Ը��ΪB1��B2����5���1��־Ը��ΪC1�����Բ����оٷ�����֪�ܹ�����Ϊ��9�֣�����ķ�����9�֣����ݹŵ���Ϳ�֪
���=5y,����ø���Ƶ�ʡ���2���ɣ�1����֪��3��4��5���Ƶ�ʷֱ�Ϊ��0.3,0.2,0.1�����Ը�������Ϊ30,20,10,���ֲ������3:2:1��ȡ�����Ե�3��4��5��ֱ��3�ˣ�2�ˣ�1�ˡ���3���ɣ�2��֪��3��4��5���зֱ��ȡ3�ˣ�2�ˣ�1�ˣ��ǵ�3���3��־Ը��ΪA1��A2��A3����4���2��־Ը��ΪB1��B2����5���1��־Ը��ΪC1�����Բ����оٷ�����֪�ܹ�����Ϊ��9�֣�����ķ�����9�֣����ݹŵ���Ϳ�֪![]() ��
��
�������:��1���������֪,��3���Ƶ��Ϊ0��06��5=0��3��
��4���Ƶ��Ϊ0��04��5=0��2��
��5���Ƶ��Ϊ0��02��5=0��1��
��2����3�������Ϊ0��3��100=30�� ��4�������Ϊ0��2��100=20��
��5�������Ϊ0��1��100=10��
��Ϊ��3��4��5�鹲��60��־Ը��,�������÷ֲ�����ķ�����60��־Ը���г�ȡ6��־Ը��,ÿ���ȡ�������ֱ�Ϊ��
������3�飺 ![]() ��6=3����4�飺
��6=3����4�飺 ![]() ��6=2����5�飺
��6=2����5�飺 ![]() ��6=1��
��6=1��
����Ӧ�ӵ�3��4��5���зֱ��ȡ3�ˣ�2�ˣ�1�ˣ� ��
��3���ǵ�3���3��־Ը��ΪA1��A2��A3����4���2��־Ը��ΪB1��B2����5���1��־Ը��ΪC1��
���6��־Ը���г�ȡ2��־Ը���У�
��A1,A2��, ��A1,A3��,��A1,B1��,��A1,B2��,��A1,C1��,��A2,A3��,��A2,B1��,��A2,B2��,��A2,C1��,��A3,B1��,��A3,B2��,
��A3,C1��,��B1,B2��,��B1,C1��,��B2,C1��������15�֣�
���е�4���2��־Ը��B1,B2������һ��־Ը�߱����е��У�
��A1,B1��, ��A1,B2��, ��A2,B1��, ��A2,B2��, ��A3,B1��, ��A3,B2��, ��B1,B2��, ��B1,C1��, ��B2,C1��������9�֣�
���Ե�4��������һ��־Ը�߱����еĸ���Ϊ![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD����ƽ����һ��P��PA��ƽ��ABCD��E��F�ֱ���AB��PC���е㣮 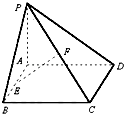
��1����֤��EF��ƽ��PAD��
��2����֤��EF��CD��
��3������PDA=45�㣬��EF��ƽ��ABCD���ɵĽǵĴ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ax2+lnx��a��R����
��1����a=![]() ʱ����f��x��������[1��e]�ϵ����ֵ����Сֵ��
ʱ����f��x��������[1��e]�ϵ����ֵ����Сֵ��
��2���������g��x����f1��x����f2��x�����ڹ���������D�ϣ�����f1��x����g��x����f2��x������ô�ͳ�g��x��Ϊf1��x����f2��x���ġ������������֪����![]() .
. ![]() ���������䣨1��+�����ϣ�����f��x����f1��x����f2��x���ġ������������a��ȡֵ��Χ��
���������䣨1��+�����ϣ�����f��x����f1��x����f2��x���ġ������������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���輯��A={x|2��5��2��x��4}��B={x|x2+2mx��3m2��0��m��0}��
��1����m=2����A��B��
��2����BA����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�����꼶��ѧ��500�ˣ���������300�ˣ�Ů��200�ˣ�Ϊ���о�ѧ������ѧ�ɼ��Ƿ����Ա��йأ��ֲ��÷ֲ�����ķ��������г�ȡ��100��ѧ������ͳ�����������п��Ե���ѧ������Ȼ���Ա��Ϊ�С�Ů���飬�ٽ�����ѧ���ķ����ֳ�5�飺[100��110����[110��120����[120��130����[130��140����[140��150]�ֱ����ͳ�ƣ��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ�� 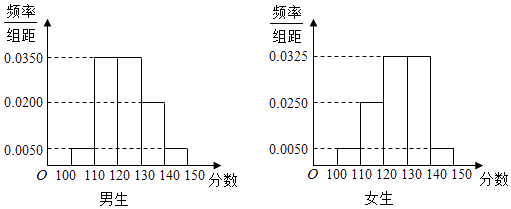
����K2= ![]() ��
��
��1���������з���С��110�ֵ�ѧ���������ȡ2�ˣ�������ǡ��Ϊһ��һŮ�ĸ��ʣ�
��2�����涨������С��130�ֵ�ѧ��Ϊ����ѧ�������������������֪�������2��2�����������ж��Ƿ���90%�İ�����Ϊ����ѧ���������Ա��йء���
P��K2��k0�� | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
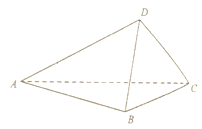
����Ŀ����֪����ABCD�ij�AB=4����AD=3�������ضԽ���BD���𣬵õ�������A��BCD����ͼ��ʾ���������н��ۣ�
��������A��BCD��������ֵΪ ![]() ��
��
��������A��BCD�����ı������Ϊ��ֵ��
����E��F�ֱ�Ϊ��AC��BD���е㣬�����EF��AC��EF��BD��
�ܵ������A��BD��CΪֱ�����ʱ��ֱ��AB��CD���ɽǵ�����ֵΪ ![]() ��
��
�ݵ������A��BD��C�Ĵ�СΪ60��ʱ����AC�ij�Ϊ ![]() ��
��
������ȷ�Ľ���������д��������ȷ���۵���ţ���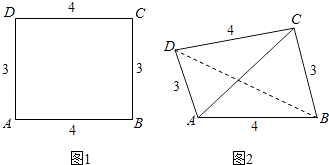
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��ABCD�У�����ABCDΪ���Σ�PA��ƽ��ABCD��EΪPD���е㣮 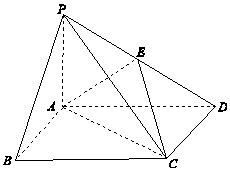
��1��֤����PB��ƽ��AEC��
��2����AP=1��AD= ![]() ������P��ABD�����V=
������P��ABD�����V= ![]() ��������D��AE��C�Ĵ�С��
��������D��AE��C�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=cos����x+�գ����أ�0����x=�� ![]() ��y=f��x������㣬ֱ��x=
��y=f��x������㣬ֱ��x= ![]() Ϊy=f��x��ͼ���һ���Գ��ᣬ�Һ���f��x�������䣨
Ϊy=f��x��ͼ���һ���Գ��ᣬ�Һ���f��x�������䣨 ![]() ��
�� ![]() ���ϵ�������ص����ֵ�ǣ� ��
���ϵ�������ص����ֵ�ǣ� ��
A.9
B.7
C.5
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����![]() �У�б��
���![]() ����
����![]() ��ֱ��
��ֱ��![]() ��ת�õ�
��ת�õ�![]() ��������
��������![]() �Ĵ�СΪ
�Ĵ�СΪ![]() .
.
��1��ȡ![]() ���е�
���е�![]() ������
������![]() ��ƽ����
��ƽ����![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ����ƽ��
����ƽ��![]() ƽ��
ƽ��![]() ʱ����
ʱ����![]() �ij���2����
�ij���2����![]() ʱ��������
ʱ��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com