练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．速度都是90km/h的甲，乙两列火车，在同一水平轨道上相向行驶，当他们距离90km时，一只燕子以150km/h的速度离开甲车车头向乙车飞去，假设燕子每次折返时都不减速，当它到达乙车车头时又立即以原速率返回，并这样继续在两车头之间来回飞，当两车头相遇时，
    （1）这只燕子一共飞行了多少千米？它在整个过程中的位移大小为多少？
    （2）燕子的平均速度是多大？平均速率是多大？

    分析 （1）先计算出火车相遇的时间，即燕子的飞行时间即可得到结论．
    （2）分别求出燕子的飞行位移和路程，即可得到结论．

    解答 解：（1）由题意知两火车从开始匀速运动到相遇需要半个小时，
    而在这半个小时里燕子一直在以150 km/h的速度匀速飞行，
    所以半个小时的时间内燕子共飞行了75 km．
    燕子在在整个过程中的位移相等于甲火车的移动位移，即90×0.5=45km．
    （2）燕子在整个过程的位移为45km，时间为0.5小时，
    则平均速度为45÷0.5=90km/h．
    燕子在整个过程的路程为75km，时间为0.5小时，
    则平均速率为75÷0.5=150km/h．

    点评 本题主要考查函数的应用问题，结合物理中的有关知识和概念是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．已知数列{2n-1•an}的前n项和Sn=1-$\frac{n}{2}$．
    （1）求数列{an}的通项公式；
    （2）设bn=$\frac{|{a}_{n}|}{n}$，求数列{$\frac{1}{{b}_{n}}$}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．设函数y=f（x）满足对任意的x∈R，f（x）≥0且f2（x+1）+f2（x）=9．已知f（$\frac{1}{2}$）=2，则f（$\frac{2015}{2}$）=$\sqrt{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知tan（$\frac{π}{4}$+α）=2．
    （1）求tanα的值；
    （2）求$\frac{1}{2sinαcosα+co{s}^{2}α}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

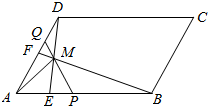    4．如图所示，在平行四边形ABCD中，$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$，$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$，BF与DE交于点M，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$．
    （1）用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{AM}$；
    （2）在线段AB上取一点P，在线段AD上取一点Q，使PQ过点M，设$\overrightarrow{AP}$=p$\overrightarrow{AB}$，$\overrightarrow{AQ}$=q$\overrightarrow{AD}$，求证：$\frac{1}{7p}$+$\frac{3}{7q}$=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知集合A={（x，y）|y=2x+1}，B={（x，y）|y=x+3}，若a∈A，a∈B，则a的值为（2，5）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．数列{an}的前n项和Sn，满足Sn=4an+1，则an=-$\frac{1}{3}$×$（\frac{4}{3}）^{n-1}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设函数y=f（x）定义域为{x|x∈R且x≠1}，已知f（x+1）为奇函数，当x＜1时，f（x）=2x2-x+1，则x＞1时，f（x）的递减区间为（　　）
    A．[$\frac{5}{4}$，+∞）B．（1，$\frac{5}{4}$]C．[$\frac{7}{4}$，+∞）D．（1，$\frac{7}{4}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=x2-2ax+a，
    （1）若f（x）≥0在R上恒成立，求a的取值范围；
    （2）若f（x）≥0在x∈[1，4]上恒成立，求a的取值范围．

    查看答案和解析>>

    同步练习册答案