练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知数列，满足：，，．

    （1）设，求数列的通项公式；

    （2）设，不等式恒成立时，求实数的取值范围．

    【答案】（1）；（2）当时，恒成立．

    【解析】

    试题分析：（1）由，化简得，得到数列是以为首项，为公差的等差数列，即可求解数列的通项公式；（2）由（1）知，，得，从而，即可求解，得到，转化为恒成立，即可满足不等式恒成立，利用二次函数的性质，即可求解实数的取值范围．

    试题解析：（1）∵，

    ∴，

    ∵，∴数列是以为首项，为公差的等差数列，

    ∴．

    （2）由（1）知，，∴，

    从而，

    ，

    ∴，

    由题意可知恒成立，即可满足不等式恒成立，

    设，

    当时，恒成立，

    当时，由的判别式，

    再结合二次函数的性质不可能成立；

    当时，对称轴，在上为单调递减函数，

    ∵，

    ∴时，恒成立．

    综上知：当时，恒成立．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥，底面是，边长为的菱形，又底面，且，点、分别是棱、的中点．

    （Ⅰ）求证： 平面；

    （Ⅱ）求证：平面平面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）记，求证：函数在区间内有且仅有一个零点；

    （2）用表示中的最小值，设函数，若关于的方程（其中为常数）在区间有两个不相等的实根，记在内的零点为，试证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的几何体中，为三棱柱，且平面，四边形为平行四边形，．

    （1）若，求证：平面；

    （2）若，二面角的余弦值为，求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

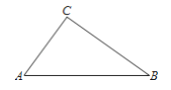
    【题目】如图，A,B,C三地有直道相通，AB=5千米，AC=3千米，BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地，经过t小时，他们之间的距离为（单位：千米）.甲的路线是AB，速度是5千米/小时，乙的路线是ACB，速度是8千米/小时，乙到达B地后原地等待，设时，乙到达C地.

    （1）求与的值；

    （2）已知警员的对讲机的有效通话距离是3千米.当时，求的表达式，并判断在上的最大值是否超过3？并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对定义在区间上的函数和，如果对任意，都有成立，那么称函数在区间上可被替代，称为“替代区间”．给出以下问题：

    ①在区间上可被替代；

    ②可被替代的一个“替代区间”为；

    ③在区间可被替代，则；

    ④（），（），则存在实数（），使得在区间上被替代； 其中真命题有 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知直线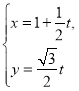：（为参数），曲线：（为参数）．

    （1）设与相交于，两点，求；

    （2）若把曲线上各点的横坐标压缩为原来的倍，纵坐标压缩为原来的倍，得到曲线，设点是曲线上的一个动点，求它到直线距离的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是数列的前n项和，满足，正项等比数列的前n项和为，且满足.

    (Ⅰ) 求数列{an}和{bn}的通项公式； (Ⅱ) 记，求数列{cn}的前n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C＝90°，D，E分别为AC，AB的中点，点F为线段CD上的一点．将△ADE沿DE折起到△A1DE的位置，使A1F⊥CD，如图2.

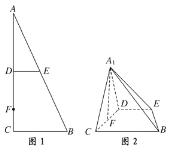
    （1）求证：DE∥平面A1CB；

    （2）求证：A1F⊥BE；

    （3）线段A1B上是否存在点Q，使A1C⊥平面DEQ？说明理由．

    查看答案和解析>>

    同步练习册答案