
 某校为了了解学生对消防知识的了解情况,从高一年级和高二年级各选取100名同学进行消防知识竞赛.图(1)和图(2)分别是对高一年级和高二年级参加竞赛的学生成绩按[40,50),[50,60),[60,70),[70,80]分组,得到的频率分布直方图.
某校为了了解学生对消防知识的了解情况,从高一年级和高二年级各选取100名同学进行消防知识竞赛.图(1)和图(2)分别是对高一年级和高二年级参加竞赛的学生成绩按[40,50),[50,60),[60,70),[70,80]分组,得到的频率分布直方图.| 成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
| 高一 | |||
| 高二 | |||
| 合计 |
| P(K2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据频率分布直方图计算高一年级学生成绩的众数和高二年级学生成绩的平均值;
(2)填写2×2列联表,计算K2,对照数表即可得出结论.
解答 解:(1)高一年级学生竞赛的众数为55(分),…(2分)
高二年级学生竞赛平均成绩为(45×15+55×35+65×35+75×15)÷100=60(分);…(4分)
(2)2×2列联表如下:
| 成绩小于6(0分)人数 | 成绩不小于6(0分)人数 | 合计 | |
| 高一年级 | 70 | 30 | 100 |
| 高二年级 | 50 | 50 | 100 |
| 合计 | 120 | 80 | 200 |
点评 本题考查了频率分布直方图的应用问题,也考查了独立性检验的应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 7 | C. | 10或4 | D. | 7或5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
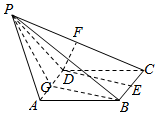 如图,椎体P-ABCD中,ABCD为边长为1的菱形,且∠DAB=60°,PA=PD=$\sqrt{2}$,PB=2,E、F、G分别为BC、PC、AD中点.
如图,椎体P-ABCD中,ABCD为边长为1的菱形,且∠DAB=60°,PA=PD=$\sqrt{2}$,PB=2,E、F、G分别为BC、PC、AD中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com