
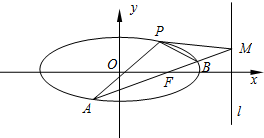
 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点(0,b)到右焦点F的距离与它到直线l:x=4的距离比恰为离心率$\frac{1}{2}$,
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点(0,b)到右焦点F的距离与它到直线l:x=4的距离比恰为离心率$\frac{1}{2}$,分析 (1)由题意将点P (1,)代入椭圆的方程,得到,再由离心率为e=$\frac{1}{2}$,将a,b用c表示出来代入方程,解得c,从而解得a,b,即可得到椭圆的标准方程;
(2)可先设出直线AB的方程为y=k(x-1),代入椭圆的方程并整理成关于x的一元二次方程,设A(x1,y1),B(x2,y2),利用根与系数的关系求得x1+x2=$\frac{8{k}^{2}}{4{k}^{2}+3}$,x1x2=$\frac{4{k}^{2}-12}{4{k}^{2}+3}$,再求点M的坐标,分别表示出k1,k2,k3.比较k1+k2=λk3即可求得参数的值;
解答 解:(1)点(0,b)到右焦点F(c,0)的距离与它到直线l:x=4的距离比恰为离心率$\frac{1}{2}$,
可得:$\frac{\sqrt{{b}^{2}+{c}^{2}}}{4}$=$\frac{1}{2}$,可得:b2+c2=4=a2,①
由离心率e=$\frac{1}{2}$,得$\frac{c}{a}$=$\frac{1}{2}$,即a=2c,则c=1,b=$\sqrt{3}$,
故椭圆的方程为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1.
(2)由题意可设AB的斜率为k,则直线AB的方程为y=k(x-1)③
代入椭圆方程$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,并整理得(4k2+3)x2-8k2x+4k2-12=0,
设A(x1,y1),B(x2,y2),
x1+x2=$\frac{8{k}^{2}}{4{k}^{2}+3}$,x1x2=$\frac{4{k}^{2}-12}{4{k}^{2}+3}$ ④
在方程③中,令x=4得,M的坐标为(4,3k),
从而k1=$\frac{{y}_{1}-\frac{3}{2}}{{x}_{1}-1}$,k2=$\frac{{y}_{2}-\frac{3}{2}}{{x}_{2}-1}$,k3=$\frac{3k-\frac{3}{2}}{4-1}$=k-$\frac{1}{2}$,
注意到A,F,B共线,则有k=kAF=kBF,即有$\frac{{y}_{1}}{{x}_{1}-1}$=$\frac{{y}_{2}}{{x}_{2}-1}$=k,
所以k1+k2=$\frac{{y}_{1}-\frac{3}{2}}{{x}_{1}-1}$+$\frac{{y}_{2}-\frac{3}{2}}{{x}_{2}-1}$=$\frac{{y}_{1}}{{x}_{1}-1}$+$\frac{{y}_{2}}{{x}_{2}-1}$-$\frac{3}{2}$($\frac{1}{{x}_{1}-1}$+$\frac{1}{{x}_{2}-1}$)
=2k-$\frac{3}{2}$×$\frac{{x}_{1}+{x}_{2}-2}{{x}_{1}{x}_{2}-({x}_{1}+{x}_{2})+1}$ ⑤
④代入⑤得k1+k2=2k-$\frac{3}{2}$×$\frac{\frac{8{k}^{2}}{4{k}^{2}+3}-2}{\frac{4{k}^{2}-12}{4{k}^{2}+3}-\frac{8{k}^{2}}{4{k}^{2}+3}+1}$=2k-1,
又k3=k-$\frac{1}{2}$,所以k1+k2=2k3
故存在常数λ=2符合题意.
点评 本题考查直线与圆锥曲线的综合问题,考查了分析转化的能力与探究的能力,考查了方程的思想,数形结合的思想,本题综合性较强,运算量大,极易出错,解答时要严谨运算,严密推理,方能碸解答出.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 20 | C. | 2$\sqrt{41}$ | D. | 4$\sqrt{41}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0•$\overrightarrow a$=0 | B. | 若$\overrightarrow a$⊥$\overrightarrow b$,则|${\overrightarrow a$+$\overrightarrow b}$|=|${\overrightarrow a$-$\overrightarrow b}$| | ||
| C. | 若$\overrightarrow a$•$\overrightarrow b$=0,则$\overrightarrow a$=$\overrightarrow 0$或$\overrightarrow b$=$\overrightarrow 0$ | D. | 若$\overrightarrow a$•$\overrightarrow b$=$\overrightarrow a$•$\overrightarrow c$,则$\overrightarrow b$=$\overrightarrow c$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2) | B. | (1,2) | C. | (1,2] | D. | (-∞,-1)∪[0,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com