
分析 (1)消去参数t,可得直线l的一般方程,根据ρ2=x2+y2,可得圆C的标准方程.
(2)判断P点位置,设A(xA,yA),B(xB,yB),利用参数方程的几何意义,求出tA+tB,tA•tB,即可求|PA|-|PB|的值.
解答 解:直线l的参数方程为$\left\{\begin{array}{l}x=1+2t\\ y=2+t\end{array}\right.$(t为参数),
消去参数t,可得x-1=2(y-2),即直线l的一般方程x-2y+3=0.
由ρ2=x2+y2,可得x2+y2=4.
即圆C的标准方程;x2+y2=4.
(1)已知P(-1,1),易知P在圆内,设A(xA,yA),B(xB,yB),
联立:$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=4}\\{\left\{\begin{array}{l}{x=1+2t}\\{y=2+t}\end{array}\right.}\end{array}\right.$
可得:tA+tB=$-\frac{8}{5}$,${t}_{A}•{t}_{B}=\frac{1}{5}>0$.
∴(1+tA)(1+tB)=$-\frac{2}{5}<0$.
两点之间的距离公式:
则|AP|=$\sqrt{5}$(1+tA).
则|BP|=$\sqrt{5}$(1+tB).
那么:|PA|-|PB|=$\sqrt{5}$|1+tA)-(1+tB)|=$\sqrt{5}$|tA+tB+2|=$\frac{2\sqrt{5}}{5}$.
点评 本题考查点的极坐标和直角坐标的互化,以及利用平面几何知识解决长度问题.利用直角坐标与极坐标间的关系.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 0 | D. | $-2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的外接球的表面积等于( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的外接球的表面积等于( )| A. | $4\sqrt{3}π$ | B. | 3π | C. | 8π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
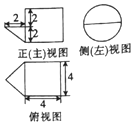
| A. | 6π | B. | $\frac{46}{3}$π | C. | 18π | D. | $\frac{52}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com