练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的外接球的表面积等于（　　）
    A．$4\sqrt{3}π$B．3πC．8πD．12π

    分析 作出棱锥的直观图，根据棱锥的结构特征得出外接球的球心位置，再计算球的表面积．

    解答 解：作出几何体的三视图如图所示：
    其中PA⊥平面ABC，AB⊥BC，PA=AB=BC=2，
    ∴PB=2$\sqrt{2}$，PC=2$\sqrt{3}$，
    ∵三棱锥的各侧面均为直角三角形，
    ∴PC为棱锥外接球的直径，
    ∴外接球的表面积S=4π×（$\frac{2\sqrt{3}}{2}$）2=12π．
    故选D．

    点评 本题考查了棱锥与外接球的位置关系，几何体的面积计算，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．已知向量$\overrightarrow{m}$=（2cos2x，$\sqrt{3}$），$\overrightarrow{n}$=（1，sin2x），设函数$f（x）=\overrightarrow m•\overrightarrow n$，则下列关于函数y=f（x）的性质的描述正确的是（　　）
    A．关于直线$x=\frac{π}{12}$对称B．关于点$（{\frac{5π}{12}，0}）$对称
    C．周期为2πD．y=f（x）在$（{-\frac{π}{3}，0}）$上是增函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．设a＞0，b＞0，且a+b≤4，则有（　　）
    A．$\frac{1}{ab}$≥$\frac{1}{2}$B．$\frac{1}{a2+b2}$≤$\frac{1}{4}$C．$\sqrt{ab}$≥2D．$\frac{1}{a}$+$\frac{1}{b}$≥1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．某四面体的三视图如图所示，该四面体的体积为（　　）
    A．$\frac{4}{3}$B．2C．$\frac{8}{3}$D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知数列{an}的首项a1=4，当n≥2时，an-1an-4an-1+4=0，数列{bn}满足bn=$\frac{1}{{2-{a_n}}}（n∈N{\;}^*）$
    （1）求证：数列{bn}是等差数列，并求{bn}的通项公式；
    （2）若cn=4bn•（nan-6），如果对任意n∈N*，都有cn+$\frac{1}{2}$t≤2t2，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

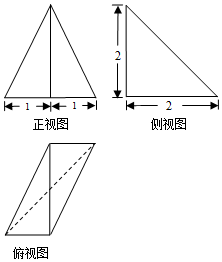    17．某三棱锥的三视图如图所示，则该三棱锥最长的棱长为（　　）
    A．$\sqrt{5}$B．$2\sqrt{2}$C．3D．$3\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．在平面直角坐标系xoy中直线l的参数方程为$\left\{\begin{array}{l}x=1+2t\\ y=2+t\end{array}\right.$（t为参数），以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，圆C的极坐标方程为ρ=2．
    （1）写出直线l的一般方程及圆C的标准方程；
    （2）设P（-1，1），直线l与圆C相交于A，B两点，求|PA|-|PB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．求函数$f（x）=sin（-2x+\frac{π}{2}）$的单调递减区间[kπ，kπ+$\frac{π}{2}$]，k∈Z．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．过点P（0，4）与抛物线y2=2x只有一个公共点的直线有3条．

    查看答案和解析>>

    同步练习册答案