
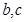 表示两条直线,
表示两条直线,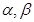 表示两个平面,则下列命题是真命题的是( )
表示两个平面,则下列命题是真命题的是( )A.若 , , ∥ ∥ ,则 ,则 ∥ ∥ |
B.若 |
C.若 ∥ ∥ , , ,则 ,则 |
D.若 |
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:不详 题型:单选题
 ,给定以下条件:
,给定以下条件: 内不共线的三点到
内不共线的三点到 的距离相等;②
的距离相等;② 是
是 内的两条直线,且
内的两条直线,且 ;
; 是两条异面直线,且
是两条异面直线,且 ;
; 的是( )
的是( )| A.① | B.② | C.①③ | D.③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 --
-- ,E、F分别是
,E、F分别是 、
、 的中点,p是
的中点,p是 上的动点(包括端点),过E、D、P作正方体的截面,若截面为四边形,则P的轨迹是
上的动点(包括端点),过E、D、P作正方体的截面,若截面为四边形,则P的轨迹是 B、线段
B、线段
 和一点
和一点 D、线段
D、线段 和一点C
和一点C查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
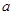 的菱形
的菱形 中,
中,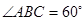 ,
,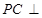 面
面 ,
,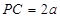 ,
,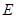 、
、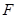 分别是
分别是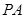 和
和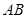 的中点.
的中点.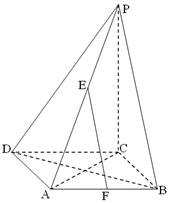
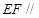 面
面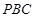 ;
; 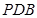 ⊥平面
⊥平面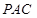 ;
;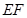 与平面
与平面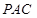 所成的角的正切值.
所成的角的正切值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com