
| A. | $\sqrt{3}$+1 | B. | 4 | C. | $\sqrt{5}$+1 | D. | 2 |
分析 求出$\overrightarrow{a},\overrightarrow{b}$的夹角,做出向量$\overrightarrow{OE}$=$\overrightarrow{a}+2\overrightarrow{b}$,则$\overrightarrow{c}$的终点C在以E为圆心,以1位半径的圆上.
解答 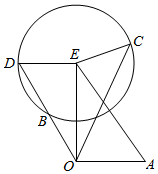 解:∵$\overrightarrow{a}$•($\overrightarrow{a}$+2$\overrightarrow{b}$)=0,∴${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}$=0,即1+2$\overrightarrow{a}•\overrightarrow{b}$=0,∴$\overrightarrow{a}•\overrightarrow{b}$=-$\frac{1}{2}$.
解:∵$\overrightarrow{a}$•($\overrightarrow{a}$+2$\overrightarrow{b}$)=0,∴${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}$=0,即1+2$\overrightarrow{a}•\overrightarrow{b}$=0,∴$\overrightarrow{a}•\overrightarrow{b}$=-$\frac{1}{2}$.
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=-$\frac{1}{2}$,∴$\overrightarrow{a},\overrightarrow{b}$的夹角为120°.
作向量$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,延长OB到D,使得$\overrightarrow{OD}=2\overrightarrow{OB}=2\overrightarrow{b}$.
以OA,OD为邻边做平行四边形OAED,则$\overrightarrow{OE}$=$\overrightarrow{a}+2\overrightarrow{b}$.设$\overrightarrow{OC}$=$\overrightarrow{c}$.
∵|$\overrightarrow{c}$-$\overrightarrow{a}$-2$\overrightarrow{b}$|=1,∴C在以E为圆心,以1位半径的圆上.
∵|OA|=1,|AE|=2,∠OAE=60°,
∴|OE|=$\sqrt{3}$,
∴|OC|的最大值为$\sqrt{3}+1$.
故选:A.
点评 本题考查了平面向量线性运算的几何意义,平面向量的数量积运算,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
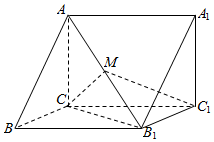 如图,在直三棱柱ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形.
如图,在直三棱柱ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 405 | B. | 540 | C. | 810 | D. | 945 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
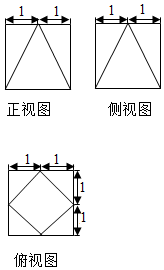 一个茶叶盒的三视图如图所示(单位:分米),盒盖与盒底为合金材料制成,其余部分为铁皮材料制成,若合金材料每平方分米造价10元,铁皮材料每平方分米造价5元,则该茶叶盒的造价为( )
一个茶叶盒的三视图如图所示(单位:分米),盒盖与盒底为合金材料制成,其余部分为铁皮材料制成,若合金材料每平方分米造价10元,铁皮材料每平方分米造价5元,则该茶叶盒的造价为( )| A. | 100元 | B. | (60+35$\sqrt{3}$)元 | C. | 130元 | D. | 200元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com