
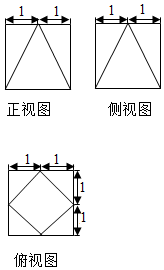
 一个茶叶盒的三视图如图所示(单位:分米),盒盖与盒底为合金材料制成,其余部分为铁皮材料制成,若合金材料每平方分米造价10元,铁皮材料每平方分米造价5元,则该茶叶盒的造价为( )
一个茶叶盒的三视图如图所示(单位:分米),盒盖与盒底为合金材料制成,其余部分为铁皮材料制成,若合金材料每平方分米造价10元,铁皮材料每平方分米造价5元,则该茶叶盒的造价为( )| A. | 100元 | B. | (60+35$\sqrt{3}$)元 | C. | 130元 | D. | 200元 |
分析 由图可以看出,茶叶盒的盒盖与盒底是正方形,边长分别为$\sqrt{2}$分米和2分米,茶叶盒形状可以看成以盒盖的边与盒底的顶点为截面切割而成,然后分别求出上下底面积与侧面面积,乘以对应的造价得答案.
解答 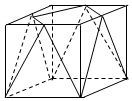 解:由图可以看出,茶叶盒的盒盖与盒底是正方形,边长分别为$\sqrt{2}$分米和2分米,
解:由图可以看出,茶叶盒的盒盖与盒底是正方形,边长分别为$\sqrt{2}$分米和2分米,
∴盒盖与盒底的面积为6平方分米;
茶叶盒形状可以看成以盒盖的边与盒底的顶点为截面切割而成,该截面的面积=$\frac{1}{2}×\sqrt{(\frac{\sqrt{2}}{2})^{2}+{2}^{2}}×\sqrt{2}=\frac{3}{2}$平方分米,
∴侧面积=4×$\frac{3}{2}+4×\frac{1}{2}×2×2=14$平方分米,
∴茶叶盒的造价=14×5+6×10=130元.
故选:C.
点评 本题考查由三视图求几何体的体积,关键是由三视图抽象出原几何体,是中档题.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
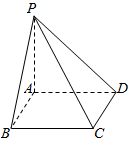 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA⊥平面ABCD.若PA=a,则直线PB与平面PCD所成的角的大小为$\frac{π}{6}$.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA⊥平面ABCD.若PA=a,则直线PB与平面PCD所成的角的大小为$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$+1 | B. | 4 | C. | $\sqrt{5}$+1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1]∪[3,+∞) | B. | (-∞,1] | C. | [3,+∞) | D. | [$\frac{3}{2}$,$\frac{11}{6}}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com