
【题目】已知数列{an}满足 ![]() an≤an+1≤3an , n∈N* , a1=1.
an≤an+1≤3an , n∈N* , a1=1.
(1)若a2=2,a3=x,a4=9,求x的取值范围;
(2)设{an}是公比为q的等比数列,Sn=a1+a2+…an , 若 ![]() Sn≤Sn+1≤3Sn , n∈N* , 求q的取值范围.
Sn≤Sn+1≤3Sn , n∈N* , 求q的取值范围.
(3)若a1 , a2 , …ak成等差数列,且a1+a2+…ak=1000,求正整数k的最大值,以及k取最大值时相应数列a1 , a2 , …ak的公差.
【答案】
(1)解:依题意: ![]() ,
,
∴ ![]() ;又
;又 ![]()
∴3≤x≤27,
综上可得:3≤x≤6
(2)解:由已知得, ![]() ,
, ![]() ,
,
∴ ![]() ,
,
当q=1时,Sn=n, ![]() Sn≤Sn+1≤3Sn,即
Sn≤Sn+1≤3Sn,即 ![]() ,成立.
,成立.
当1<q≤3时, ![]() ,
, ![]() Sn≤Sn+1≤3Sn,即
Sn≤Sn+1≤3Sn,即 ![]() ,
,
∴ ![]()
不等式 ![]()
∵q>1,故3qn+1﹣qn﹣2=qn(3q﹣1)﹣2>2qn﹣2>0对于不等式qn+1﹣3qn+2≤0,令n=1,
得q2﹣3q+2≤0,
解得1≤q≤2,又当1≤q≤2,q﹣3<0,
∴qn+1﹣3qn+2=qn(q﹣3)+2≤q(q﹣3)+2=(q﹣1)(q﹣2)≤0成立,
∴1<q≤2,
当 ![]() 时,
时,
![]() ,
, ![]() Sn≤Sn+1≤3Sn,即
Sn≤Sn+1≤3Sn,即 ![]() ,
,
∴此不等式即 ![]() ,
,
3q﹣1>0,q﹣3<0,
3qn+1﹣qn﹣2=qn(3q﹣1)﹣2<2qn﹣2<0,
qn+1﹣3qn+2=qn(q﹣3)+2≥q(q﹣3)+2=(q﹣1)(q﹣2)>0
∴ ![]() 时,不等式恒成立,
时,不等式恒成立,
上,q的取值范围为: ![]()
(3)解:设a1,a2,…ak的公差为d.由 ![]() ,且a1=1,
,且a1=1,
得 ![]()
即 ![]()
当n=1时,﹣ ![]() ≤d≤2;
≤d≤2;
当n=2,3,…,k﹣1时,由 ![]() ,得d≥
,得d≥ ![]() ,
,
所以d≥ ![]()
![]() ,
,
所以1000=k ![]() ,即k2﹣2000k+1000≤0,
,即k2﹣2000k+1000≤0,
得k≤1999
所以k的最大值为1999,k=1999时,a1,a2,…ak的公差为﹣ ![]()
【解析】(1)依题意: ![]() ,又
,又 ![]() 将已知代入求出x的范围;(2)先求出通项:
将已知代入求出x的范围;(2)先求出通项: ![]() ,由
,由 ![]() 求出
求出 ![]() ,对q分类讨论求出Sn分别代入不等式
,对q分类讨论求出Sn分别代入不等式 ![]() Sn≤Sn+1≤3Sn , 得到关于q的不等式组,解不等式组求出q的范围.(3)依题意得到关于k的不等式,得出k的最大值,并得出k取最大值时a1 , a2 , …ak的公差.
Sn≤Sn+1≤3Sn , 得到关于q的不等式组,解不等式组求出q的范围.(3)依题意得到关于k的不等式,得出k的最大值,并得出k取最大值时a1 , a2 , …ak的公差.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系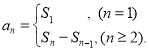 ,以及对等比数列的基本性质的理解,了解{an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列.
,以及对等比数列的基本性质的理解,了解{an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列.


科目:高中数学 来源: 题型:
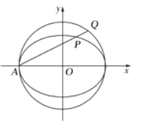
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,长轴长为4,过椭圆的左顶点
,长轴长为4,过椭圆的左顶点![]() 作直线
作直线![]() ,分别交椭圆和圆
,分别交椭圆和圆![]() 于相异两点
于相异两点![]()
(1) 若直线![]() 的斜率为1,求
的斜率为1,求![]() 的值:
的值:
(2) 若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax2﹣bx﹣1,其中a,b∈R,e=2.71828…为自然对数的底数.
(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑到倾斜的木板上(人可看作质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70o、90o和105o,则( )

A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能确定t1、t2、t3之间的关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个人有n把钥匙,其中只有一把可以打开房门,他随意的进行试开,若试开过的钥匙放在一边,试开次数X为随机变量,则P(X=k)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求证:![]()
(2)若函数![]() 的图象与直线
的图象与直线![]() 没有交点,求实数
没有交点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,则是否存在实数
,则是否存在实数![]() ,使得
,使得![]() 的最小值为
的最小值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com