练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】为了更好地支持“中小型企业”的发展，某市决定对部分企业的税收进行适当的减免，某机构调查了当地的中小型企业年收入情况，并根据所得数据画出了样本的频率分布直方图，下面三个结论：

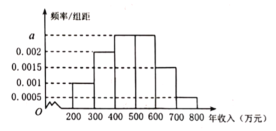
    ①样本数据落在区间的频率为0.45；

    ②如果规定年收入在500万元以内的企业才能享受减免税政策，估计有55%的当地中小型企业能享受到减免税政策；

    ③样本的中位数为480万元.

    其中正确结论的个数为（ ）

    A.0B.1C.2D.3

    【答案】D

    【解析】

    根据直方图求出，求出的频率，可判断①；求出的频率，可判断②；根据中位数是从左到右频率为的分界点，先确定在哪个区间，再求出占该区间的比例，求出中位数，判断③.

    由，，

    的频率为，①正确；

    的频率为，②正确；

    的频率为，的频率为，

    中位数在且占该组的，

    故中位数为，③正确.

    故选:D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】去年年底，某商业集团公司根据相关评分细则，对其所属25家商业连锁店进行了考核评估.将各连锁店的评估分数按[60,70), [70,80), [80,90), [90,100),分成四组，其频率分布直方图如下图所示，集团公司依据评估得分，将这些连锁店划分为A,B,C,D四个等级，等级评定标准如下表所示.

    评估得分

    [60,70)

    [70,80)

    [80,90)

    [90,100)

    评定等级

    D

    C

    B

    A

    （1）估计该商业集团各连锁店评估得分的众数和平均数；

    （2）从评估分数不小于80分的连锁店中任选2家介绍营销经验，求至少选一家A等级的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平行四边形中，，，，是EA的中点（如图1），将沿CD折起到图2中的位置，得到四棱锥是．

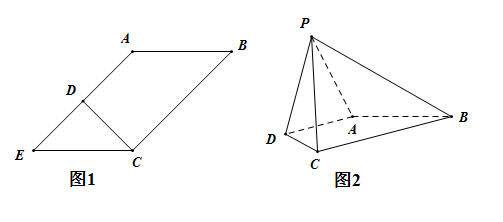
    （1）求证：平面PDA；

    （2）若PD与平面ABCD所成的角为．且为锐角三角形，求平面PAD和平面PBC所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和为，（为常数）对于任意的恒成立．

    （1）若，求的值；

    （2）证明：数列是等差数列；

    （3）若，关于的不等式有且仅有两个不同的整数解，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，是正方形，点在以为直径的半圆弧上（不与，重合），为线段的中点，现将正方形沿折起，使得平面平面.

    （1）证明：平面.

    （2）若，当三棱锥的体积最大时，求到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，分别在轴，轴上运动，，点在线段上，且.

    （1）求点的轨迹的方程；

    （2）直线与交于，两点，，若直线，的斜率之和为2，直线是否恒过定点？若是，求出定点的坐标；若不是，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）求函数在上的单调区间；

    （2）用表示中的最大值，为的导函数，设函数，若在上恒成立，求实数的取值范围；

    （3）证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设O为坐标原点，动点M在椭圆C上，过M作x轴的垂线，垂足为N，点P满足.

    （1）求点P的轨迹方程；

    （2）设点在直线上，且.证明：过点P且垂直于OQ的直线过C的左焦点F.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：，动直线l与椭圆E交于不同的两点，，且△AOB的面积为1，其中O为坐标原点.

    （1）证明：为定值；

    （2）设线段AB的中点为M，求的最大值.

    查看答案和解析>>

    同步练习册答案