
分析 要充分利用图形的直观性,熟练利用向量加法的三角形法则进行运算.
解答 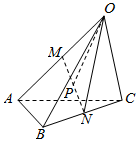 解:如图,连接ON,在△OMN中,点P是MN中点,
解:如图,连接ON,在△OMN中,点P是MN中点,
则由平行四边形法则得$\overrightarrow{OP}$=$\frac{1}{2}$($\overrightarrow{OM}$+$\overrightarrow{ON}$)
=$\frac{1}{2}$$\overrightarrow{OM}$+$\frac{1}{2}$$\overrightarrow{ON}$=$\frac{1}{4}$$\overrightarrow{OA}$+$\frac{1}{2}$•$\frac{1}{2}$($\overrightarrow{OB}$+$\overrightarrow{OC}$)
=$\frac{1}{4}$$\overrightarrow{OA}$+$\frac{1}{4}$$\overrightarrow{OB}$+$\frac{1}{4}$$\overrightarrow{OC}$,
∴λ+μ+γ=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 本题考查空间向量的运算,即向量加法的平行四边形法则,三角形法则,空间向量基基底的概念,空间向量的基本定理及其意义.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
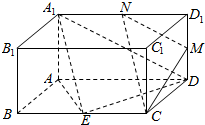 如图,长方体ABCD-A1B1C1D1中,AA1=AB=1,AD=2,E为BC的中点,点M,N分别为棱DD1,A1D1的中点.
如图,长方体ABCD-A1B1C1D1中,AA1=AB=1,AD=2,E为BC的中点,点M,N分别为棱DD1,A1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-x2+2x | B. | y=x+$\frac{1}{x}$ | C. | y=2x-2-x | D. | y=1-$\sqrt{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
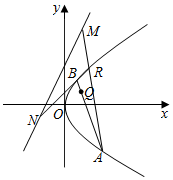 已知抛物线C的方程为y2=2px(p>0),抛物线的焦点到直线l:y=2x+2的距离为$\frac{4\sqrt{5}}{5}$.
已知抛物线C的方程为y2=2px(p>0),抛物线的焦点到直线l:y=2x+2的距离为$\frac{4\sqrt{5}}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com