
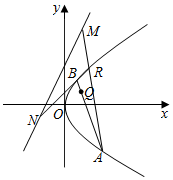
 已知抛物线C的方程为y2=2px(p>0),抛物线的焦点到直线l:y=2x+2的距离为$\frac{4\sqrt{5}}{5}$.
已知抛物线C的方程为y2=2px(p>0),抛物线的焦点到直线l:y=2x+2的距离为$\frac{4\sqrt{5}}{5}$.分析 (Ⅰ)可以得到抛物线的焦点为$(\frac{p}{2},0)$,而根据点到直线的距离公式得到$\frac{|p+2|}{\sqrt{5}}=\frac{4\sqrt{5}}{5}$,而由p>0即可得出p=2,从而得出抛物线方程为y2=4x;
(Ⅱ)容易求出R点坐标为(1,2),可设AB:x=m(y-1)+1,$A(\frac{1}{4}{{y}_{1}}^{2},{y}_{1}),B(\frac{1}{4}{{y}_{2}}^{2},{y}_{2})$,直线AB方程联立抛物线方程消去x可得到y2-4my+4m-4=0,从而有y1+y2=4m,y1y2=4m-4.可写出直线AR的方程,联立y=2x+2即可得出${x}_{M}=-\frac{2}{{y}_{1}}$,而同理可得到${x}_{N}=-\frac{2}{{y}_{2}}$,这样即可求出$|MN|=2\sqrt{5}\sqrt{1+\frac{1}{m+\frac{1}{m}-2}}$,从而看出m=-1时,|MN|取到最小值$\sqrt{15}$,并且可得出此时直线AB的方程.
解答 解:(Ⅰ)抛物线的焦点为$(\frac{p}{2},0)$,$d=\frac{{|{p+2}|}}{{\sqrt{5}}}=\frac{{4\sqrt{5}}}{5}$,得p=2,或-6(舍去);
∴抛物线C的方程为y2=4x;
(Ⅱ)点R(x0,2)在抛物线C上;
∴x0=1,得R(1,2);
设直线AB为x=m(y-1)+1(m≠0),$A(\frac{1}{4}{{y}_{1}}^{2},{y}_{1})$,$B(\frac{1}{4}{{y}_{2}}^{2},{y}_{2})$;
由$\left\{\begin{array}{l}{x=m(y-1)+1}\\{{y}^{2}=4x}\end{array}\right.$得,y2-4my+4m-4=0;
∴y1+y2=4m,y1y2=4m-4;
AR:$y-2=\frac{{y}_{1}-2}{\frac{1}{4}{{y}_{1}}^{2}-1}(x-1)$=$\frac{4}{{y}_{1}+2}(x-1)$;
由$\left\{\begin{array}{l}{y-2=\frac{4}{{y}_{1}+2}(x-1)}\\{y=2x+2}\end{array}\right.$,得${x_M}=-\frac{2}{y_1}$,同理${x_N}=-\frac{2}{y_2}$;
∴$|{MN}|=\sqrt{5}|{{x_M}-{x_N}}|=2\sqrt{5}|{\frac{1}{y_2}-\frac{1}{y_1}}|=2\sqrt{5}\frac{{\sqrt{{m^2}-m+1}}}{{|{m-1}|}}=2\sqrt{5}\sqrt{1+\frac{m}{{{m^2}-2m+1}}}$=$2\sqrt{5}\sqrt{1+\frac{1}{{m-2+\frac{1}{m}}}}$;
∴当m=-1时,${|{MN}|_{min}}=\sqrt{15}$,此时直线AB方程:x+y-2=0.
点评 考查抛物线的标准方程,抛物线的焦点坐标,以及点到直线的距离公式,曲线上的点的坐标和曲线方程的关系,过定点的直线方程的设法,以及直线的点斜式方程,韦达定理,弦长公式,复合函数的单调性,要清楚函数$y=x+\frac{1}{x}$的单调性.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的最小正周期为2π | |
| B. | f(x)的图象关于直线x=$\frac{π}{2}$对称 | |
| C. | 函数f(x)在区间上(-$\frac{π}{12}$,$\frac{5π}{12}$)是增函数 | |
| D. | 由函数y=3sin2x的图象向右平移$\frac{π}{3}$个单位长度可得到函数f(x)的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | -$\frac{1}{8}$ | C. | -$\frac{\sqrt{3}}{8}$ | D. | -$\frac{3}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 3 | 4 | 5 | 6 |
| y | $\frac{5}{2}$ | m | 4 | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {1,3,4} | C. | {1,4,5} | D. | {2,3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com