
分析 (1)根据正弦定理化简已知的等式,由sinA不等于0,两边除以sinA,得到sinC的值,由C的范围,利用特殊角的三角函数值即可求出角C的度数.
(2)由已知利用三角形面积个数可求b,进而可求a,利用余弦定理即可解得c的值.
解答 解:(1)∵由a=2csinA,
∴根据正弦定理得:sinA=2sinCsinA,
又∵sinA≠0,得到sinC=$\frac{1}{2}$,又C∈(0,π),
∴则角C的大小为$\frac{π}{6}$或$\frac{5π}{6}$.
又∵c<a,可得C为锐角,
∴C=$\frac{π}{6}$
(2)∵C=$\frac{π}{6}$,a=$\frac{2\sqrt{3}}{3}$b,△ABC的面积为$\frac{\sqrt{3}}{2}$,
∴$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$×$\frac{2\sqrt{3}}{3}$b×b×$\frac{1}{2}$,解得:b=$\sqrt{3}$,a=2,
∴由余弦定理可得:c=$\sqrt{{a}^{2}+{b}^{2}-2abcosC}$=$\sqrt{4+3-2×2×\sqrt{3}×\frac{\sqrt{3}}{2}}$=1
点评 此题考查学生灵活运用正弦定理及特殊角的三角函数值化简求值,考查了三角形面积公式,余弦定理在解三角形中的应用,属于基础题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:解答题
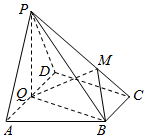 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=AD=2,BC=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=AD=2,BC=1,CD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2$\sqrt{3}$,2$\sqrt{3}$) | B. | (2$\sqrt{3}$,+∞) | C. | (-2$\sqrt{3}$,0)∪(2$\sqrt{3}$,+∞) | D. | (-2$\sqrt{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2+4x-y+4=0 | B. | x2+y2+2x-3y+4=0 | C. | x2+y2+4x-3y+4=0 | D. | x2+y2+4x-3y+5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 2 | C. | -9 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 135° | B. | 45° | C. | 135°或45° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,四边形BDCE内接于以BC为直径的⊙A,已知:$BC=10,cos∠BCD=\frac{3}{5},∠BCE=30°$,则线段DE的长是( )
如图,四边形BDCE内接于以BC为直径的⊙A,已知:$BC=10,cos∠BCD=\frac{3}{5},∠BCE=30°$,则线段DE的长是( )| A. | $\sqrt{89}$ | B. | 7$\sqrt{3}$ | C. | 4+3$\sqrt{3}$ | D. | 3+4$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com