【题目】给定无穷数列
，若无穷数列
满足：对任意
，都有
，则称与“接近”.
（1）设是首项为
，公比为的等比数列，
，，判断数列是否与接近，并说明理由；
（2）已知是公差为
的等差数列，若存在数列
满足：与接近，且在
这100个值中，至少有一半是正数，求的取值范围.
【答案】（1）数列
与
是接近的，详见解析（2）
【解析】
（1）写出与的通项公式，计算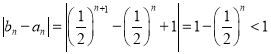
即可证明（2）由题意
，分公差
，公差
，
，公整
分类讨论，分别取满足条件
，利用
与接近的定义，计算
中所含的正数.
（1）数列与是接近的.理由如下：
因为是首项为
公比为的等比数列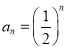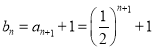，所以
，
，所以，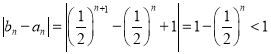
，
即数列与是接近的.
（2）因为是公差为
的等差数列，若存在数列满足：与是接近的，
可得，
①若公差，可取
，可得
，
则中有100个正数，符合题意；
②若公差，取
，则
，，
，
则中有100个正数，符合题意；
③若公差，可令
，
，
，
则
中有50个正数，符合题意；
④若公整，若存在数列满足：与是接近的，
即为
，
，
可得
，
则中无正数，不符合题意；
综上：的取值范围是.
寒假天地重庆出版社系列答案科目：高中数学 来源： 题型：
【题目】某工厂利用随机数表对生产的600个零件进行抽样测试，先将600个零件进行编号，编号分别为001，002，
，599，600从中抽取60个样本，如下提供随机数表的第4行到第6行：
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若从表中第6行第6列开始向右依次读取3个数据，则得到的第6个样本编号
A. 522B. 324C. 535D. 578
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）＝|x﹣2|﹣t，t∈R，g（x）＝|x+3|．
（1）x∈R，有f（x）≥g（x），求实数t的取值范围；
（2）若不等式f（x）≤0的解集为[1，3]，正数a、b满足ab﹣2a﹣b＝2t﹣2，求a+2b的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P﹣ABCD中，△PAD为正三角形，AB∥CD，AB=2CD，∠BAD=90°，PA⊥CD，E为棱PB的中点
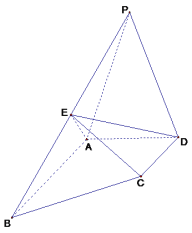
（1）求证：平面PAB⊥平面CDE；
（2）若AD=CD=2，求点P到平面ADE的距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的前
项和
满足
.
(1)证明数列
为等差数列，并求出数列的通项公式.
(2)若不等式
，对任意
恒成立，求
的取值范围.
(3)记数列
的前项和为
，是否存在正整数
，使得
成立，若存在，求出所有符合条件的有序实数对(，)；若不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
