
分析 (Ⅰ)通过对数的运算性质可知bn=n•anlga,进而利用错位相减法计算即得结论;
(Ⅱ)通过分析可知bn≤bn+1恒成立,进而分0<a<1与a>1两种情况讨论即可.
解答 解:(Ⅰ)依题意,an=an,
当n≥2时,bn=Sn-Sn-1=lg${{a}_{n}}^{{a}_{n}}$=anlgan=n•anlga,
又∵b1=alga满足上式,
∴bn=n•anlga,
则Sn=(1•a+2•a2+…+n•an)lga,
aSn=[1•a2+2•a3+…+(n-1)•an+n•an+1]lga,
两式相减得:(1-a)Sn=(a+a2+a3+…+an-n•an+1)lga
=[$\frac{a(1-{a}^{n})}{1-a}$-n•an+1]lga
=$\frac{a-(1+n-na)•{a}^{n+1}}{1-a}$•lga,
∴Sn=$\frac{a-(1+n-na)•{a}^{n+1}}{(1-a)^{2}}$•lga;
(Ⅱ)依题意,对任意的n,有bn≤bn+1,
∴n•anlga≤(n+1)an+1lga,即nlga≤(n+1)alga,
当0<a<1时,lga<0,此时n≥(n+1)a,
∴a≤$\frac{n}{n+1}$,
∴0<a≤$\frac{1}{2}$;
当a>1时,lga>0,此时n≤(n+1)a,
∴a≥$\frac{n}{n+1}$,
∴a>1;
综上所述,0<a≤$\frac{1}{2}$或a>1.
点评 本题考查数列的通项及前n项和,考查错位相减法,考查分类讨论的思想,注意解题方法的积累,属于中档题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
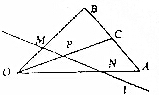 如图,在△AOB中,OC是边AB的中线,P是OC的中点,直线l与OB,OA分别交于点M,N,若$\overrightarrow{OM}$=$\frac{3}{8}$$\overrightarrow{OB}$,$\overrightarrow{OA}$=x$\overrightarrow{ON}$,则x=( )
如图,在△AOB中,OC是边AB的中线,P是OC的中点,直线l与OB,OA分别交于点M,N,若$\overrightarrow{OM}$=$\frac{3}{8}$$\overrightarrow{OB}$,$\overrightarrow{OA}$=x$\overrightarrow{ON}$,则x=( )| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{2}^{2015}}$ | B. | -$\frac{1}{{2}^{2015}}$ | C. | -22015 | D. | 22015 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com