
【题目】设函数f(x)=ax3-3ax,g(x)=bx2-ln x(a,b∈R),已知它们在x=1处的切线互相平行.
(1)求b的值;
(2)若函数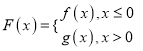 且方程F(x)=a2有且仅有四个解,求实数a的取值范围.
且方程F(x)=a2有且仅有四个解,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)
【解析】试题分析:(1)由![]() 和
和![]() 在
在![]() 处的切线互相平行得,
处的切线互相平行得, ![]() ,解方程求出
,解方程求出![]() 值.
值.
(2)分别求出求出![]() 的极值和
的极值和![]() 的极值,结合单调性画出
的极值,结合单调性画出![]() 的图象,结合图象可得若方程
的图象,结合图象可得若方程![]() 有四个解,则
有四个解,则 ![]() ,解不等式求得实数
,解不等式求得实数![]() 的取值范围.
的取值范围.
试题解析:函数g(x)=bx2-ln x的定义域为(0,+∞),
(1)f′(x)=3ax2-3af′(1)=0,
g′(x)=2bx-![]() g′(1)=2b-1,
g′(1)=2b-1,
依题意得2b-1=0,所以b=![]() .
.
(2)x∈(0,1)时,g′(x)=x-![]() <0,
<0,
即g(x)在(0,1)上单调递减,
x∈(1,+∞)时,g′(x)=x-![]() >0,即g(x)在(1,+∞)上单调递增,所以当x=1时,g(x)取得极小值g(1)=
>0,即g(x)在(1,+∞)上单调递增,所以当x=1时,g(x)取得极小值g(1)=![]() ;当a=0时,方程F(x)=a2不可能有四个解;
;当a=0时,方程F(x)=a2不可能有四个解;
当a<0,x∈(-∞,-1)时,f′(x)<0,即f(x)在(-∞,-1)上单调递减,x∈(-1,0)时,f′(x)>0,
即f(x)在(-1,0)上单调递增,
所以当x=-1时,f(x)取得极小值f(-1)=2a,
又f(0)=0,所以F(x)的图象如图①所示,

从图象可以看出F(x)=a2不可能有四个解.
当a>0,x∈(-∞,-1)时,f′(x)>0,
即f(
x∈(-1,0)时,f′(x)<0,
即f(x)在(-1,0)上单调递减,
所以当x=-1时,f(x)取得极大值f(-1)=2a.又f(0)=0,所以F(x)的图象如图②所求,

从图②看出,若方程F(x)=a2有四个解,则![]() <a2<2a,
<a2<2a,
得![]() <a<2,
<a<2,
所以,实数a的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知向量![]() ,函数
,函数![]() ,且
,且![]() 图象上一个最高点为
图象上一个最高点为![]() 与
与![]() 最近的一个最低点的坐标为
最近的一个最低点的坐标为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设![]() 为常数,判断方程
为常数,判断方程![]() 在区间
在区间![]() 上的解的个数;
上的解的个数;
(Ⅲ)在锐角![]() 中,若
中,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在以坐标原点为极点,![]() 轴的正半轴为极轴建立的极坐标系中,曲线
轴的正半轴为极轴建立的极坐标系中,曲线![]() 的参数方程
的参数方程![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程:
的极坐标方程:![]() .
.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 交
交![]() 轴于点
轴于点![]() (不是原点),过点
(不是原点),过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于A,B两个不同的点,求
于A,B两个不同的点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次学科测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.

则参加测试的总人数为______,分数在![]() 之间的人数为______.
之间的人数为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示是一个正方体的平面展开图,在这个正方体中![]() 平面ADE;
平面ADE;![]() 平面ABF;
平面ABF;![]() 平面
平面![]() 平面AFN;
平面AFN;![]() 平面
平面![]() 平面NCF.以上四个命题中,真命题的序号是
平面NCF.以上四个命题中,真命题的序号是![]()
![]()
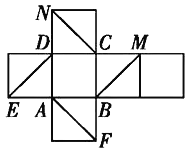
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
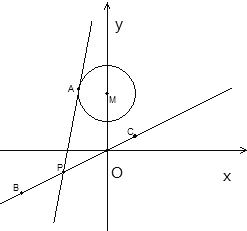
【题目】已知圆M:![]() ,设点B,C是直线l:
,设点B,C是直线l:![]() 上的两点,它们的横坐标分别是t,
上的两点,它们的横坐标分别是t,![]() ,P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A
,P点的纵坐标为a且点P在线段BC上,过P点作圆M的切线PA,切点为A
![]() 若
若![]() ,
,![]() ,求直线PA的方程;
,求直线PA的方程;
![]() 经过A,P,M三点的圆的圆心是D,
经过A,P,M三点的圆的圆心是D,
![]() 将
将![]() 表示成a的函数
表示成a的函数![]() ,并写出定义域.
,并写出定义域.
![]() 求线段DO长的最小值.
求线段DO长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99%的把握认为“喜爱打篮球与性别有关”?说明你的理由.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com