
分析 先联立已知的两条直线方程求出交点的坐标,由直线l与两坐标轴的截距互为相反数,分两种情况考虑:
①当直线l与坐标轴的截距不为0时,设出直线l的截距式方程x-y=a,把交点坐标代入即可求出a的值,得到直线l的方程;
②当直线l与坐标轴的截距为0时,设直线l的方程为y=kx,把交点坐标代入即可求出k的值,得到直线l的方程.
解答 解:联立已知的两直线方程得:$\left\{\begin{array}{l}{3x+2y-1=0}\\{5x+2y+1=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$,
所以两直线的交点坐标为(-1,2),
因为直线l在两坐标轴上的截距互为相反数,
①当直线l与坐标轴的截距不为0时,可设直线l的方程为:x-y=a,
直线l过两直线的交点,所以把(-1,2)代入直线l得:a=-3,则直线l的方程为x-y=-3即x-y+3=0;
②当直线l与两坐标的截距等于0时,设直线l的方程为y=kx,
直线l过两直线的交点,所以把(-1,2)代入直线l得:k=-2,所以直线l的方程为y=-2x即2x+y=0.
综上①②,直线l的方程为x-y+3=0或2x+y=0.
点评 此题考查学生会根据两直线的方程求两直线的交点坐标,考查了分类讨论的数学思想,是一道综合题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 已知圆心坐标为$(1,\sqrt{3})$的圆M与y轴及直线y=$\frac{{\sqrt{3}}}{3}$x相切于A、B两点,另一圆N1与圆M外切(圆N1在圆M的斜上方),且与y轴及直线y=$\frac{{\sqrt{3}}}{3}$x分别切于C、D两点.(如图)
已知圆心坐标为$(1,\sqrt{3})$的圆M与y轴及直线y=$\frac{{\sqrt{3}}}{3}$x相切于A、B两点,另一圆N1与圆M外切(圆N1在圆M的斜上方),且与y轴及直线y=$\frac{{\sqrt{3}}}{3}$x分别切于C、D两点.(如图)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
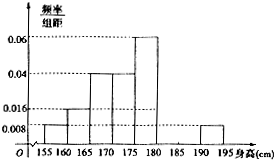 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪N | B. | M∩N | C. | ∁IM∪∁IN | D. | ∁IM∩∁IN |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{3}$ | C. | -3 | D. | -$\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com