
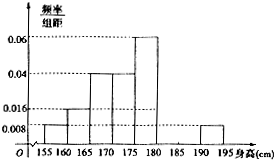
 ��ijѧУ��800�������������ȡ50���������ߣ�����ѧ������ȫ������155cm��195cm֮�䣬��������������·�ʽ�ֳɰ��飺��һ��[155��160�����ڶ���[160��165���������ڰ���[190��195]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪��һ����ڰ���������ͬ�������������Ϊ4�ˣ�
��ijѧУ��800�������������ȡ50���������ߣ�����ѧ������ȫ������155cm��195cm֮�䣬��������������·�ʽ�ֳɰ��飺��һ��[155��160�����ڶ���[160��165���������ڰ���[190��195]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪��һ����ڰ���������ͬ�������������Ϊ4�ˣ����� ��1�����ɵ�����������������������õ��������Ƶ�ʣ�Ȼ����1��ȥ��������������Ƶ�ʺͼ��ɵõ��������Ƶ�ʣ���Ϊ����λ����ֱ������ľ��ε������ȣ�������ǰ�����Ƶ�ʺ�С��0.5���������Ƶ�ʺʹ���0.5���ɴ˶϶���λ��λ�ڵ����飬�����λ��m����0.04+0.08+0.2+��m-170����0.04=0.5���������λ��m��ֵ��
��2���ֱ����������͵ڰ���������������оٷ��г����������ڵ�����͵ڰ�������������������ȡ�����������ܵķ������ٸ��ݹŵ���͵ĸ��ʹ�ʽ��֮���ɣ�
��� �⣺��1���������Ƶ��Ϊ$\frac{4}{50}=0.08$����1��
�������Ƶ��Ϊ1-0.08-5����0.08��2+0.016+0.04��2+0.06��=0.06����3�֣�
��֪��λ��λ��[170��175]֮����Ϊm�����У�m-170����0.04=0.5-0.32=0.18��m=174.5
������180cm���ϣ���180cm��������Ϊ0.18��800=144�ˡ���6�֣�
��2��������[180��185��������Ϊ4�ˣ���Ϊa��b��c��d��
�ڰ���[190��195]������Ϊ2�ˣ���ΪA��B��
����г�ȡ������ab��ac��ad��bc��bd��cd��aA��bA��cA��dA��aB��bB��cB��dB��AB��15�������
���¼�E={|x-y|��5}�������ҽ��������ȡ������������ͬһ�飬
�����¼�E�����Ļ����¼�Ϊab��ac��ad��bc��bd��cd��AB��7�������
��$P=\frac{7}{15}$����12�֣�
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ���������оٷ�������¼����¼������ĸ��ʣ�������Ĺؼ�����ȷƵ��ֱ��ͼ�и����ε�Ƶ�ʺ͵���1����λ����Ƶ�ʷֲ�ֱ��ͼ�У����õ��ֱ�߰Ѹ�����������ֵĵ�ĺ����꣬�����ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1+i | B�� | 1 | C�� | $\sqrt{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
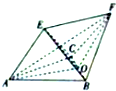 ��ͼ��ʾ���ڶ�����EF-ABC�У���ABC�DZ߳�Ϊ2�ĵȱ������Σ�OΪBC���е㣬EF��AO��EA=EC=EF=$\sqrt{3}$��
��ͼ��ʾ���ڶ�����EF-ABC�У���ABC�DZ߳�Ϊ2�ĵȱ������Σ�OΪBC���е㣬EF��AO��EA=EC=EF=$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | r��$\frac{1}{2}$ | B�� | $\frac{1}{2}$��r��$\frac{3}{2}$ | C�� | r��$\frac{3}{2}$ | D�� | r��$\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com