
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
分析 先看当A、B都在左支上时,若AB垂直x轴,根据双曲线方程求得焦点的坐标,把焦点横坐标代入双曲线方程求得交点的纵坐标,进而求得AB的长小于5,则考虑不垂直于x轴的两条;再看若A、B分别在两支先看A,B为两顶点时,不符合题意进而可推断出符合题意的直线有两条,最后综合可得答案.
解答 解:①若A、B都在右支,
若AB垂直x轴,a2=4,b2=2,c2=6,所以F($\sqrt{6}$,0)
则AB:x=$\sqrt{6}$,
代入双曲线线$\frac{x^2}{4}$-$\frac{y^2}{2}$=1求得y=±$\frac{4}{\sqrt{6}}$,
所以AB=|y1-y2|=$\frac{8}{\sqrt{6}}$<5,不成立;
若A,B不垂直于x轴,则有两条直线满足;
②若A、B分别在两支,
a=2,所以顶点距离为2+2=4<5,所以|AB|=5有两条,关于x轴对称.
所以一共4条.
故选:D.
点评 本题主要考查了双曲线的对称性和直线与双曲线的关系.考查了学生分析推理和分类讨论思想的运用.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
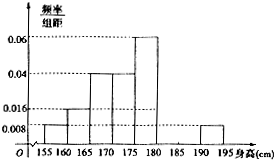 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $6\sqrt{3}$ | B. | $8\sqrt{3}$ | C. | $18\sqrt{3}$ | D. | $8\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com