
分析 $\frac{y-2}{x-1}$表示圆上的点P(x,y)与点M(1,2)连线的斜率,设为k,则过点M的圆的切线方程为y-2=k(x-1),由圆心到切线的距离等于半径,求得k的值,可得$\frac{y-2}{x-1}$的最大值.
解答 解:$\frac{y-2}{x-1}$表示圆上的点P(x,y)与点M(1,2)连线的斜率,
设为k,则过点M的圆的切线方程为y-2=k(x-1),
即 kx-y+2-k=0,由圆心到切线的距离等于半径,可得$\frac{|-2k-0+2-k|}{\sqrt{{k}^{2}+1}}$=1,求得k=$\frac{3±\sqrt{3}}{4}$,
故$\frac{y-2}{x-1}$的最大值为$\frac{3+\sqrt{3}}{4}$.
故答案为:$\frac{3+\sqrt{3}}{4}$.
点评 本题主要考查直线的斜率公式,直线和圆相切的性质,点到直线的距离公式的应用,体现了转化的数学思想,属于基础题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:选择题
| A. | “|x|>1”是“x>1”的必要不充分条件. | |
| B. | 若命题p:?x∈R,2x<3.则¬p:?x∈R,2x≥3. | |
| C. | 若p∧q为假命题,则p∨q也为假命题. | |
| D. | 命题“若x+y≠5,则x≠2或y≠3”是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-cos2x | B. | y=-2sin2x | C. | y=-2cos2x | D. | y=sin(2x-$\frac{π}{4}$)-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
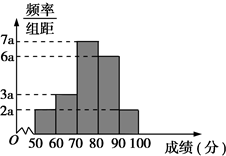 20名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com