
【题目】已知双曲线![]() ,抛物线
,抛物线![]() ,
, ![]() 与
与![]() 有公共的焦点
有公共的焦点![]() ,
, ![]() 与
与![]() 在第一象限的公共点为
在第一象限的公共点为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,且
,且![]() ,则关于双曲线的离心率的说法正确的是()
,则关于双曲线的离心率的说法正确的是()
A. 仅有两个不同的离心率![]() 且
且![]() B. 仅有两个不同的离心率
B. 仅有两个不同的离心率![]() 且
且![]() C. 仅有一个离心率
C. 仅有一个离心率![]() 且
且![]() D. 仅有一个离心率
D. 仅有一个离心率![]() 且
且![]()
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:
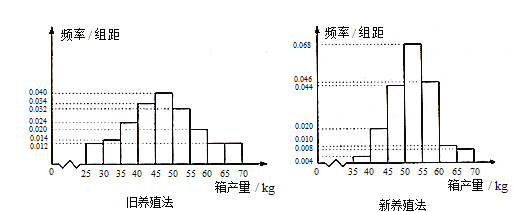
(1) 记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;
(2) 填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3) 根据箱产量的频率分布直方图,对两种养殖方法的优劣进行较。
附:
P( | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,BC⊥平面APC,AB=2 ![]() ,AP=PC=CB=2.
,AP=PC=CB=2. 
(1)求证:AP⊥平面PBC;
(2)求二面角P﹣AB﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )过点
)过点![]() ,
, ![]() 、
、![]() 分别为其左、右焦点,
分别为其左、右焦点, ![]() 为坐标原点,点
为坐标原点,点![]() 为椭圆上一点,
为椭圆上一点, ![]() 轴,且
轴,且![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆![]() 的离心率和方程;
的离心率和方程;
(Ⅱ)设![]() 、
、![]() 是椭圆上两动点,若直线
是椭圆上两动点,若直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 ![]() =2csinA
=2csinA
(1)确定角C的大小;
(2)若c= ![]() ,且△ABC的面积为
,且△ABC的面积为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面9m,拱圈内水面宽22m.一条船在水面以上部分高6.5m,船顶部宽4m,故通行无阻.近日水位暴涨了2.7m,为此,必须加重舰载,降低船身,才能通过桥洞.试问船身至少应该降低多少?(精确到0.01,参考数据: ![]() )
) 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行乒乓球决赛,比赛采取七局四胜制.现在的情形是甲胜3局,乙胜2局.若两人胜每局的概率相同,则甲获得冠军的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com