
分析 首先分析题目求在面积为S的△ABC的边AB上任取一点P,则△PAC的面积大于$\frac{S}{3}$的概率,可考虑画图求解的方法,然后根据图形分析出基本的事件空间与事件的几何度量是什么.再根据几何关系求解出它们的比例即可.
解答 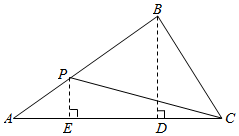 解:记事件Ω={△PAC的面积大于$\frac{S}{3}$},
解:记事件Ω={△PAC的面积大于$\frac{S}{3}$},
基本事件空间是线段AB的长度,(如图
因为S△PAC≥$\frac{1}{3}{S}_{△ABC}$,则有$\frac{1}{2}AC•PE>\frac{1}{3}×\frac{1}{2}AC•BD$;
化简记得到$\frac{PE}{BD}>\frac{1}{3}$:,因为PE∥BD,则由三角形的相似性$\frac{AP}{AB}>\frac{1}{3}$;
所以,事件Ω的几何度量为线段BP的长度,
因为AP=$\frac{1}{3}$AB,
所以P(Ω)=$\frac{BP}{AB}$=$\frac{2}{3}$;
故答案为:$\frac{2}{3}$.
点评 解决有关几何概型的问题的关键是认清基本事件空间是指面积还是长度或体积,同学们需要注意.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 处罚金额x(单位:元) | 0 | 5 | 10 | 15 | 20 |
| 会闯红灯的人数y | 80 | 50 | 40 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-2i | B. | 1+2i | C. | $\frac{5}{3}$-$\frac{10}{3}$i | D. | $\frac{5}{3}$+$\frac{10}{3}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
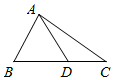 如图,在△ABC中,角A,B,C所对的边分别为a,b,c,($\frac{1}{4}$a-sinC)cosB=sinBcosC,b=4$\sqrt{3}$.
如图,在△ABC中,角A,B,C所对的边分别为a,b,c,($\frac{1}{4}$a-sinC)cosB=sinBcosC,b=4$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com