
分析 (1)求导数,对c讨论,即可得出函数f(x)的单调性.
(2)若f(x)≤x2恒成立,$c≥\frac{lnx}{x}-x$,?x∈(0,+∞),构造函数,求最大值,即可求c的取值范围.
解答 解:(1)∵f(x)=ln x-cx,
∴x∈(0,+∞),f′(x)=$\frac{1-cx}{x}$.
c≤0时,f(x)在(0,+∞)单调递增;
c>0时f(x)在$(0\;,\;\frac{1}{c})$单调递增,$(\frac{1}{c}\;,\;+∞)$单调递减 …6
(2)lnx-cx≤x2,?x∈(0,+∞)
∴$c≥\frac{lnx}{x}-x$,?x∈(0,+∞)
令$F(x)=\frac{{{{ln}^x}}}{x}-x$,$F'(x)=\frac{{1-{{ln}^x}}}{{x{\;}^2}}-1=\frac{{1-{{ln}^x}-{x^2}}}{x^2}$,
F'(1)=0,?x∈(0,1),F'(x)>0;
x∈(1,+∞),F'(x)<0,
∴F(x)在(0,1)单调递增,在 (1,+∞)单调递减,
∴Fmax=F(1)=-1,
∴c≥-1,
即c的取值范围为[-1,+∞).…12
点评 本题考查函数的单调性,考查恒成立问题,正确分离参数求最大值是关键.


科目:高中数学 来源: 题型:解答题
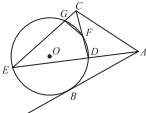 如图,AB是⊙O的一条切线,切点为B,直线ADE、CFD、CGE都是⊙O的割线,已知AC=AB.
如图,AB是⊙O的一条切线,切点为B,直线ADE、CFD、CGE都是⊙O的割线,已知AC=AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不是充分条件也不是必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
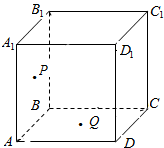 如图所示,已知P,Q是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.
如图所示,已知P,Q是正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD的中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com