
����Ŀ��������������ָʵ�ʲ��������������ı��ʣ���r�����������Ǻ�����ҵ������Ӫ״������Ҫָ�꣮��ͼΪ����ͳ�ƾַ�����2015����2018���2�����ҹ���ҵ���������ʵ�����ͼ��
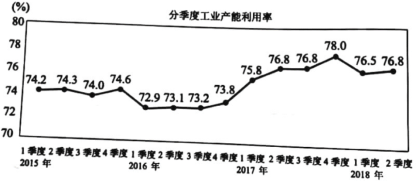
��ͳ��ѧ�У�ͬ����ָ����ͳ����������һ��ͬ��ͳ��������Ƚϣ�����2016��ڶ�������2015��ڶ�������Ƚϣ�������ָ����ͳ������������ͳ��������Ƚϣ�����2015��ڶ�������2015���һ������Ƚϣ�
��������Ϣ�����н�������ȷ���ǣ� ����
A. 2015��������Ȼ����������B. 2016���һ����ͬ���������
C. 2017���������ͬ���������D. 2018���һ���Ȼ����������
���𰸡�C
��������
����ͬ�Ⱥͻ��ȵĶ���Ƚ��������ݵó����ۣ�
�⣺2015��ڶ�����������Ϊ74.3%����������������Ϊ74.0%����2015��������Ȼ��������½�����A����
2015���һ����������Ϊ74.2%��2016���һ����������Ϊ72.9%����2016���һ����ͬ�������½�����B����
2016�����������������Ϊ73.2%��2017���������������Ϊ76.8%����2017���������ͬ��������ߣ���C��ȷ��
2017����ļ���������Ϊ78%��2018���һ����������Ϊ76.5%����2018���һ���Ȼ��������½�����D����
��ѡ��C��


 �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ��
��![]() ��������
��������![]() .
.
����![]() ʱ���жϺ���
ʱ���жϺ���![]() �Ƿ��м�ֵ��
�Ƿ��м�ֵ��
����Ҫʹ����![]() �ļ�Сֵ�����㣬�����
�ļ�Сֵ�����㣬�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�������ԣ����������ȡֵ��Χ�ڵ����⺯��![]() ������
������![]() ������
������![]() �ڶ�������������ʵ��
�ڶ�������������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ˬ���ҹ��Ŵ���ѧ�ҡ�����ѧ�Ҵ�Լ�ڹ�Ԫ222����ˬΪ���ܱ��㾭��һ������ʱ�������ˡ�����Բ��ͼ������ơ���ˬ��ͼ��(����Ϊ�߳��õ�������������4��ȫ�ȵ�ֱ���������ټ����м��һ��С��������ɵ�)��ȡ���ˬ��ͼ������ˬ��ͼ�����Ƶع�����ͼ��ʾ��ͼ�Σ������ɸ�3ȫ�ȵĵȱ����������м��һ��С�ȱ���������ɵ�һ����ȱ������Σ���DF2AF�����ڴ�ȱ������������ȡһ�㣬��˵�ȡ��С�ȱ������εĸ�����( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �Ķ���Ϊԭ�㣬�佹��
�Ķ���Ϊԭ�㣬�佹��![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() ����
����![]() Ϊֱ��
Ϊֱ��![]() �ϵĵ㣬����
�ϵĵ㣬����![]() ��������
��������![]() ����������
����������![]() ������
������![]() Ϊ�е㣮
Ϊ�е㣮
(1) ��������![]() �ķ��̣�
�ķ��̣�
(2) ����![]() Ϊֱ��
Ϊֱ��![]() �ϵĶ���ʱ����ֱ��
�ϵĶ���ʱ����ֱ��![]() �ķ��̣�
�ķ��̣�
(3) ����![]() ��ֱ��
��ֱ��![]() ���ƶ�ʱ����
���ƶ�ʱ����![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����![]() ��
��![]() ��������������ͬ���Ʒ������Ʒ����һ���������ȼ����࣬��ÿ���ɷֱ����10Ԫ��8Ԫ��6Ԫ���ִ�
��������������ͬ���Ʒ������Ʒ����һ���������ȼ����࣬��ÿ���ɷֱ����10Ԫ��8Ԫ��6Ԫ���ִ�![]() ��
��![]() �����ߵIJ�Ʒ�и������ȡ100�����м�⣬���ͳ������ͼ��
�����ߵIJ�Ʒ�и������ȡ100�����м�⣬���ͳ������ͼ��
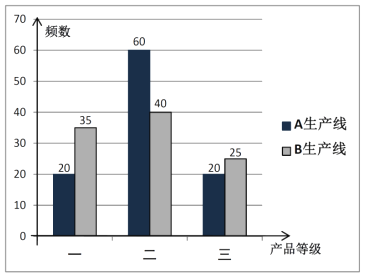
��1��������֪���ݣ��ж��Ƿ���99%�İ�����Ϊһ�ȼ���Ʒ���������йأ�
��2���ֱ�������������߳�����Ʒ�����ķ���Դ���Ϊ�ж����ݣ�˵�����������ߵĻ������ȶ���
��3�����Ƹó�����Ϊ2000����Ʒʱ�������Լ�һ�ȼ���Ʒ������.
����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��![]() ����
����![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣮
���㣮
��1����![]() ���ܳ���
���ܳ���
��2�����![]() Ϊ��Բ
Ϊ��Բ![]() ���϶��㣬��
���϶��㣬��![]() �ڵ�һ���ޣ���
�ڵ�һ���ޣ���![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() �����
�����![]() �ĺ����ꣻ
�ĺ����ꣻ
��3����ֱ��![]() ��ƽ���������ᣬ��
��ƽ���������ᣬ��![]() Ϊ��
��![]() ����
����![]() ��ĶԳƵ㣬ֱ��
��ĶԳƵ㣬ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ��������ֵ��
��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l�IJ�������Ϊ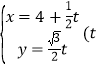 Ϊ����
Ϊ����![]() ��������ԭ��Ϊ���㣬x���������Ϊ���Ὠ����������ϵ������C�ļ����귽��Ϊ
��������ԭ��Ϊ���㣬x���������Ϊ���Ὠ����������ϵ������C�ļ����귽��Ϊ![]() ��
��
![]() ������C��ֱ�����귽����ֱ��l�ļ����귽�̣�
������C��ֱ�����귽����ֱ��l�ļ����귽�̣�
![]() ��
��![]() ��ֱ��
��ֱ��![]() ������C���ڵ�
������C���ڵ�![]() ��ͬ��ԭ��
��ͬ��ԭ��![]() ����ֱ��l���ڵ�B����
����ֱ��l���ڵ�B����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����ln��x2+1����e��|x|��eΪ��Ȼ�����ĵ���������ʽf��2x+1����f��x���Ľ⼯�ǣ�������
A. ����1��1��B. �����ޣ���1���ȣ�1��+�ޣ�
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() ��
��![]() ��ʹ�ò���ʽ
��ʹ�ò���ʽ![]() ����������
����������![]() �IJ���ʽ
�IJ���ʽ![]() �Ľ⼯��Ϊ
�Ľ⼯��Ϊ![]() .
.
��1����![]() Ϊ�棬��ʵ��
Ϊ�棬��ʵ��![]() ��ȡֵ����
��ȡֵ����![]() ��
��
��2���ڣ�1���������£���![]() ��
��![]() �ij�ֲ���Ҫ��������ʵ��
�ij�ֲ���Ҫ��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com