Question

定义在R上的函数y=f（x）是偶函数，当x≥0时，f（x）=-4x²+8x-3．
（Ⅰ）当x＜0时，求f（x）的解析式；
（Ⅱ）求y=f（x）的最大值，并写出f（x）在R上的单调区间（不必证明）．

Answer 1

解：（Ⅰ）设x＜0，则-x＞0，
f（-x）=-4（-x）²+8（-x）-3=-4x²-8x-3，
∵f（x）是偶函数，∴f（-x）=f（x），
∴x＜0时，f（x）=-4x²-8x-3．
（Ⅱ）由（Ⅰ）知，
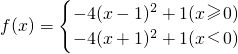
∴y=f（x）开口向下，所以y=f（x）有最大值f（1）=f（-1）=1．
函数y=f（x）的单调递增区间是（-∞，-1]和[0，1]；
单调递减区间是[-1，0]和[1，+∞）．
分析：（Ⅰ）x＜0时，-x＞0，代入已知x≥0时，f（x）=-4x²+8x-3，可得f（-x）=-4x²-8x-3，根据偶函数的性质可求得f（x）=-4x²-8x-3；
（Ⅱ）根据二次函数的单调性分别求解两段函数的单调区间即可．
点评：本题主要考查了利用偶函数的对称性求解函数的解析式，函数单调性的判断与证明，函数的单调区间的求解，（Ⅱ）中对每段函数求解单调区间时要注意函数的定义域．
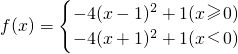