
分析 (I)运用离心率公式和点到直线的距离公式,解方程可得a,b,进而得到椭圆方程;
(Ⅱ)在x轴上假设存在异于F的一点G,设为(n,0),设直线l的方程为y=k(x-n),代入椭圆方程x2+2y2=2,运用韦达定理,以及三点共线的条件:斜率相等,化简整理,可得n=2,进而判断存在G(2,0).
解答 解:(I)由题意可得e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
直线AB的方程为bx+ay=ab,
由题意可得$\frac{|ab|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{\sqrt{6}}{3}$,
又a2-b2=c2,解得a=$\sqrt{2}$,b=c=1,即有椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1;
(Ⅱ)在x轴上假设存在异于F的一点G,设为(n,0),
设直线l的方程为y=k(x-n),代入椭圆方程x2+2y2=2,
可得(1+2k2)x2-4nk2x+2k2n2-2=0,
设M(x1,y1),N(x2,y2),
可得x1+x2=$\frac{4n{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{2{k}^{2}{n}^{2}-2}{1+2{k}^{2}}$,
由假设可得P(x1,-y1),F(1,0),N(x2,y2)三点共线,可得
kPN=kNF,即$\frac{{y}_{2}+{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{{y}_{2}}{{x}_{2}-1}$,
由y1=k(x1-n),y2=k(x2-n),可得
(x1+x2-2n)(x2-1)=(x2-x1)(x2-n),
化简为(n+1)(x1+x2)-2x1x2-2n=0,
即有(n+1)•$\frac{4n{k}^{2}}{1+2{k}^{2}}$-2•$\frac{2{k}^{2}{n}^{2}-2}{1+2{k}^{2}}$-2n=0,
化简可得n=2,
代入判别式可得2k2<1,故存在异于F的一点G,且为(2,0),
使N、F、P三点共线.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和点到直线的距离公式,考查存在性问题的解法,注意运用直线和椭圆方程联立,运用韦达定理和三点共线的条件:斜率相等,考查化简整理的运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
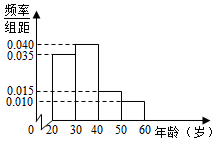 某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20,30) | 30 | 18 |
| [30,40) | 36 | 24 |
| [40,50) | 12 | 9 |
| [50,60] | 4 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0)为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,点P在椭圆C上,且△PF1F2面积的最大值为$\sqrt{3}$.
已知F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0)为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,点P在椭圆C上,且△PF1F2面积的最大值为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 生二孩 | 不生二孩 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com