
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:填空题
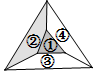 《数学万花筒》第7页中谈到了著名的“四色定理”.问题起源于1852年的伦敦大学学院毕业生弗朗西斯•加斯里.他给自己的弟弟弗莱德里克写的信中提到:“可以使用四种(或更少)颜色为平面上画出的每张地图着色,使任何相邻的两个地区的边界线具有不同的颜色吗?”回答他这个问题用了124年,但简单的图形我们能用逐一列举的方法解决.若用红、黄、蓝、绿四种颜色给右边的地图着色,假定区域①已着红色,区域②已着黄色,则剩余的区域③④共有2种着色方法.
《数学万花筒》第7页中谈到了著名的“四色定理”.问题起源于1852年的伦敦大学学院毕业生弗朗西斯•加斯里.他给自己的弟弟弗莱德里克写的信中提到:“可以使用四种(或更少)颜色为平面上画出的每张地图着色,使任何相邻的两个地区的边界线具有不同的颜色吗?”回答他这个问题用了124年,但简单的图形我们能用逐一列举的方法解决.若用红、黄、蓝、绿四种颜色给右边的地图着色,假定区域①已着红色,区域②已着黄色,则剩余的区域③④共有2种着色方法.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{10}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{5}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 909 | B. | 910 | C. | 911 | D. | 912 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com