
设函数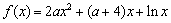 .
.
(Ⅰ)若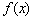 在x=
在x=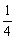 处的切线与直线4x+y=0平行,求a的值;
处的切线与直线4x+y=0平行,求a的值;
(Ⅱ)讨论函数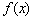 的单调区间;
的单调区间;
(Ⅲ)若函数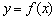 的图象与x轴交于A,B两点,线段AB中点的横坐标为
的图象与x轴交于A,B两点,线段AB中点的横坐标为 ,证明
,证明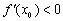 .
.
解:(I)由题知f(x)=2ax2+(a+4)x+lnx的定义域为(0,+∞),
且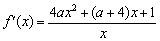 .
.
又∵ f(x)的图象在x=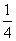 处的切线与直线4x+y=0平行,
处的切线与直线4x+y=0平行,
∴ 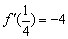 ,
,
解得 a=-6.
(Ⅱ)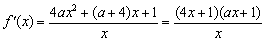 ,
,
由x>0,知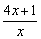 >0.
>0.
①当a≥0时,对任意x>0,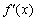 >0,
>0,
∴ 此时函数f(x)的单调递增区间为(0,+∞).
②当a<0时,令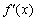 =0,解得
=0,解得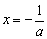 ,
,
当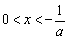 时,
时,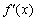 >0,当
>0,当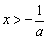 时,
时,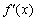 <0,
<0,
此时,函数f(x)的单调递增区间为(0,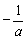 ),单调递减区间为(
),单调递减区间为(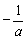 ,+∞).
,+∞).
(Ⅲ)不妨设A(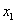 ,0),B(
,0),B(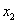 ,0),且
,0),且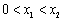 ,由(Ⅱ)知
,由(Ⅱ)知 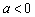 ,
,
于是要证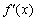 <0成立,只需证:
<0成立,只需证: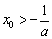 即
即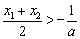 .
.
∵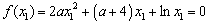 , ①
, ①
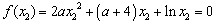 , ②
, ②
①-②得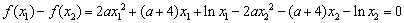 ,
,
即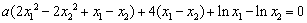 ,
,
∴ 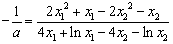 ,
,
故只需证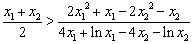 ,
,
即证明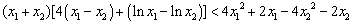 ,
,
即证明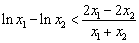 ,变形为
,变形为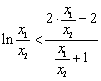 ,
,
设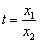
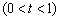 ,令
,令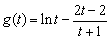 ,
,
则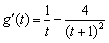
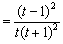 ,
,
显然当t>0时,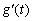 ≥0,当且仅当t=1时,
≥0,当且仅当t=1时,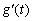 =0,
=0,
∴ g(t)在(0,+∞)上是增函数.
又∵ g(1)=0,
∴ 当t∈(0,1)时,g(t)<0总成立,命题得证.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com