练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知关于x的不等式kx2﹣2x+3k＜0．
    （1）若不等式的解集为{x|x＜﹣3或x＞﹣1}，求k的值；
    （2）若不等式的解集为，求实数k的取值范围．

    【答案】
    （1）解：由不等式的解集为{x|x＜﹣3或x＞﹣1}，

    可知k＜0，﹣3和﹣1是一元二次方程kx2﹣2x+3k=0的两根，

    所以 ，

    解得k=﹣


    （2）解：因不等式kx2﹣2x+3k＜0的解集为，

    若k=0，则不等式﹣2x＜0，

    此时x＞0，不合题意；

    若k≠0，则 ，

    解得 ；

    综上，实数k的取值范围是（0， ]


    【解析】（1）根据不等式与对应一元二次方程的关系，利用根与系数的关系求出k的值；（2）根据不等式kx2﹣2x+3k＜0的解集为，讨论k的取值，求出结果即可．
    【考点精析】利用解一元二次不等式对题目进行判断即可得到答案，需要熟知求一元二次不等式解集的步骤：一化：化二次项前的系数为正数;二判：判断对应方程的根;三求：求对应方程的根;四画：画出对应函数的图象;五解集：根据图象写出不等式的解集;规律：当二次项系数为正时，小于取中间，大于取两边．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=1﹣ （x∈R），
    （1）求反函数f﹣1（x）；
    （2）解不等式f﹣1（x）＞log2（1+x）+1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在等比数列{an}中，公比q≠1，等差数列{bn}满足a1=b1=3，a2=b4 ， a3=b13 ．
    （1）求数列{an}的{bn}通项公式；
    （2）记cn=anbn ， 求数列{cn}的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数y=sin（2x+ ）cos（x﹣ ）+cos（2x+ ）sin（ ﹣x）的图象的一条对称轴方程是（ ）
    A.x=
    B.x=
    C.x=π
    D.x=

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知具有相关关系的两个变量之间的几组数据如下表所示：

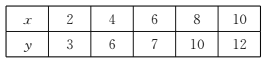
    （1）请根据上表数据在网格纸中绘制散点图；

    （2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程，并估计当时， 的值；

    （3）将表格中的数据看作五个点的坐标，从这五个点中随机抽取2个点，求这两个点都在直线的右下方的概率.

    （参考公式： ， ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】己知数列{an}的前n项和Sn= ，n∈N* ．
    （1）求数列{an}的通项公式；
    （2）设bn=2an+（﹣1）nan ， 求数列{bn}的前2n项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业准备投入适当的广告费对产品进行促销，在一年内预计销售Q（万件）与广告费x（万元）之间的函数关系为Q= （x≥0）．已知生产此产品的年固定投入为3万元，每生产1万元此产品仍需再投入32万元，若每件销售价为“平均每件生产成本的150%”与“年平均每件所占广告费的50%”之和．
    （1）试将年利润W（万元）表示为年广告费x（万元）的函数；
    （2）当年广告费投入多少万元时，企业年利润最大？最大利润为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知一元二次函数f（x）=ax2+bx+c（a＞0，c＞0）的图象与x轴有两个不同的公共点，其中一个公共点的坐标为（c，0），且当0＜x＜c时，恒有f（x）＞0．
    （1）当a=1， 时，求出不等式f（x）＜0的解；
    （2）求出不等式f（x）＜0的解（用a，c表示）；
    （3）若以二次函数的图象与坐标轴的三个交点为顶点的三角形的面积为8，求a的取值范围；
    （4）若不等式m2﹣2km+1+b+ac≥0对所有k∈[﹣1，1]恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中真命题的个数为（ ）
    ①命题“若lgx=0，则x=l”的逆否命题为“若lgx≠0，则x≠1”
    ②若“p∧q”为假命题，则p，q均为假命题
    ③命题p：x∈R，使得sinx＞l；则￢p：x∈R，均有sinx≤1
    ④“x＞2”是“ ＜ ”的充分不必要条件．
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    同步练习册答案