
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上有解,求
上有解,求![]() 的取值范围;
的取值范围;
(3)设![]() 是函数
是函数![]() 的导函数,
的导函数,![]() 是函数
是函数![]() 的导函数,若函数
的导函数,若函数![]() 的零点为
的零点为![]() ,则点
,则点![]() 恰好就是该函数
恰好就是该函数![]() 的对称中心.试求
的对称中心.试求![]() 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某中学学校对高三年级文科学生进行了一次自主学习习惯的自评满意度的调查,按系统抽样方法得到了一个自评满意度(百分制,单位:分)的样本,如图分别是该样本数据的茎叶图和频率分布直方图(都有部分缺失).
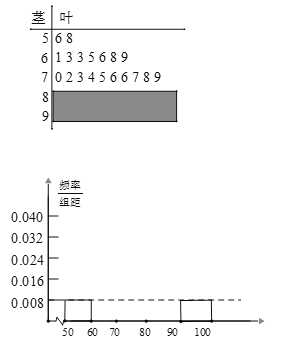
(1)完善频率分布直方图(需写出计算过程);
(2)分别根据茎叶图和频率分布直方图求出样本数据的中位数m1和m2,并指出选用哪一个数据来估计总体的中位数更合理(需要叙述理由).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水污染现状与工业废水排放密切相关,某工厂深人贯彻科学发展观,努力提高污水收集处理水平,其污水处理程序如下:原始污水必先经过A系统处理,处理后的污水(A级水)达到环保标准(简称达标)的概率为p(0<p<1).经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
某厂现有4个标准水量的A级水池,分别取样、检测,多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有样本不达标,则混合样本的化验结果必不达标,若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放
现有以下四种方案:
方案一:逐个化验;
方案二:平均分成两组化验;方案三;三个样本混在一起化验,剩下的一个单独化验;
方案四:四个样本混在一起化验.
化验次数的期望值越小,则方案越"优".
(1)若![]() ,求2个A级水样本混合化验结果不达标的概率;
,求2个A级水样本混合化验结果不达标的概率;
(2)①若![]() ,现有4个A级水样本需要化验,请问:方案一、二、四中哪个最“优"?②若“方案三”比“方案四"更“优”,求p的取值范围.
,现有4个A级水样本需要化验,请问:方案一、二、四中哪个最“优"?②若“方案三”比“方案四"更“优”,求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义一:对于一个函数![]() ,若存在两条距离为d的直线
,若存在两条距离为d的直线![]() 和
和![]() ,使得在
,使得在![]() 时,
时,![]() 恒成立,则称函数
恒成立,则称函数![]() 在D内有一个宽度为d的通道.定义二:若一个函数
在D内有一个宽度为d的通道.定义二:若一个函数![]() ,对于任意给定的正数
,对于任意给定的正数![]() ,都存在一个实数
,都存在一个实数![]() ,使得函数
,使得函数![]() 在
在![]() 内有一个宽度为
内有一个宽度为![]() 的通道,则称
的通道,则称![]() 在正无穷处有永恒通道.下列函数:①
在正无穷处有永恒通道.下列函数:①![]() ;②
;②![]() ;③
;③![]() .其中在正无穷处有永恒通道的函数的个数为( )
.其中在正无穷处有永恒通道的函数的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
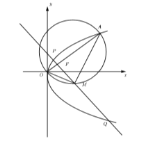
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线上异于原点的任意一点,以
为抛物线上异于原点的任意一点,以![]() 为直径作圆
为直径作圆![]() ,当直线
,当直线![]() 的斜率为1时,
的斜率为1时,![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过焦点![]() 作
作![]() 的垂线
的垂线![]() 与圆
与圆![]() 的一个交点为
的一个交点为![]() ,
,![]() 交抛物线于
交抛物线于![]() ,
,![]() (点
(点![]() 在点
在点![]() ,
,![]() 之间),记
之间),记![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水箱用的“浮球”是由两个相同半球和一个圆柱筒组成,它的轴截面如图所示,已知半球的直径是![]() ,圆柱筒高
,圆柱筒高![]() ,为增强该“浮球”的牢固性,给“浮球”内置一“双蝶形”防压卡,防压卡由金属材料杆
,为增强该“浮球”的牢固性,给“浮球”内置一“双蝶形”防压卡,防压卡由金属材料杆![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 及
及![]() 焊接而成,其中
焊接而成,其中![]() ,
,![]() 分别是圆柱上下底面的圆心,
分别是圆柱上下底面的圆心,![]() ,
,![]() ,
,![]() ,
,![]() 均在“浮球”的内壁上,AC,BD通过“浮球”中心
均在“浮球”的内壁上,AC,BD通过“浮球”中心![]() ,且
,且![]() 、
、![]() 均与圆柱的底面垂直.
均与圆柱的底面垂直.
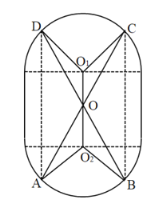
(1)设![]() 与圆柱底面所成的角为
与圆柱底面所成的角为![]() ,试用
,试用![]() 表示出防压卡中四边形
表示出防压卡中四边形![]() 的面积
的面积![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
(2)研究表明,四边形![]() 的面积越大,“浮球”防压性越强,求四边形
的面积越大,“浮球”防压性越强,求四边形![]() 面积取最大值时,点
面积取最大值时,点![]() 到圆柱上底面的距离
到圆柱上底面的距离![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司统计了2010~2018年期间公司年收的增加值![]() (万元)以及相应的年增长率
(万元)以及相应的年增长率![]() ,所得数据如下所示:
,所得数据如下所示:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
增加值 | 1555 | 2100 | 2220 | 2740 | 3135 | 3563 | 4041 | 5494.4 | 6475 |
增长率 |
|
|
|
|
|
|
|
|
|
(1)通过散点图可知,可用线性回归模型拟合2010~2014年![]() 与
与![]() 的关系;
的关系;
①求2010~2014年这5年期间公司年利润的增加值的平均数![]() ;
;
②求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)从哪年开始连续三年公司利润增加值的方差最大?(不需要说明理由)
附:参考公式:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为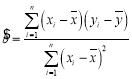 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
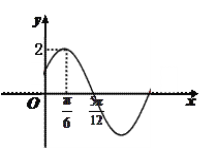
(1) 求函数![]() 的解析式;
的解析式;
(2) 如何由函数![]() 的通过适当图象的变换得到函数
的通过适当图象的变换得到函数![]() 的图象, 写出变换过程;
的图象, 写出变换过程;
(3) 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com