
分析 根据数列{an}的前n项之和公式,观察可知是等差数列,求得a1=2,d=2,求得an,写出cn的通项公式,再利用乘x,错位相减,求Tn.
解答 解:(1)由Sn=n2+n可知a1=2,数列{an}是等差数列d=2,
∴an=2n;
(2)cn=2nxn-1
Tn=2+4x+6x2+8x3+…+2nxn-1,①
则xTn=2x+4x2+6x3+8x4+…+2nxn,②
①-②,得(1-x)Tn=2+2x+2x2+…+2xn-1-2nxn,
当x≠1时,(1-x)Tn=2×$\frac{1-{x}^{n}}{1-x}$-2nxn
Tn=$\frac{2-2(n+1){x}^{n}+2n{x}^{n+1}}{(1-x)^{2}}$
当x=1时,Tn=2+4+6+8+…+2n=n2+n.
总上可知,
$\left\{\begin{array}{l}{{n}^{2}+n}&{n=1}\\{\frac{2-2(n+1){x}^{n}+2n{x}^{n+1}}{(1-x)^{2}}}&{n≠1}\end{array}\right.$
Tn=
点评 本题考查等差数列求通项公式,求数列的前n项和采用错位相减法,属于中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $S_{23}^{\;}$ | B. | S24 | C. | S25 | D. | S26 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
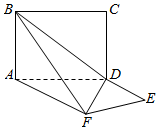 平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为30°.
平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,则异面直线EF与BC所成角大小为30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com