
直三棱柱ABC-A1B1C1中, AC=BC=AA1=2,∠ACB=90°.E为BB1的中点,D点在AB上且DE=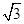 .
.
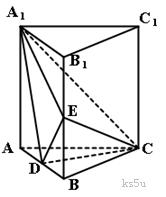
(Ⅰ)求证:CD⊥平面A1ABB1;
(Ⅱ)求三棱锥A1-CDE的体积.
(1)见解析 (2)三棱锥A1-CDE的体积为1.
【解析】(1)证明线面垂直根据判断定理,只需要证明直线垂直这个平面内的两条相交直线即可.本小题可以证明CD⊥AB, CD⊥AA1即可.
(2)本小题求面积不易直接求,采用整体减去部分的作法求解.本小题可以用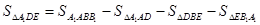 求解
求解
(1)在Rt△DBE中,BE=1,DE=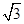 ,∴BD=
,∴BD=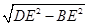 =
=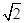 =
=
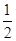 AB,
AB,
∴ 则D为AB中点, 而AC=BC, ∴CD⊥AB
又∵三棱柱ABC-A1B1C1为直三棱柱, ∴CD⊥AA1
又 AA1∩AB=A 且 AA1、AB Ì 平面A1ABB1
故 CD⊥平面A1ABB1 6分
(2)∵四边形A1ABB1为矩形,∴△A1AD,△DBE,△EB1A1都是直角三角形,
∴ 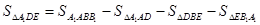
=2×2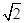 -
-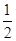 ×
×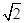 ×2-
×2-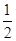 ×
×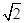 ×1-
×1-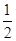 ×2
×2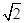 ×1=
×1=
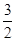
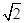
∴ VA1-CDE =VC-A1DE = 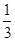 ×SA1DE ×CD=
×SA1DE ×CD= 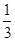 ×
×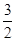
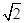 ×
×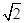 =1
=1
∴ 三棱锥A1-CDE的体积为1


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
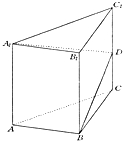 如图,已知直三棱柱ABC-A1B1C1,侧棱长为2,底面△ABC中,∠B=90°,AB=1,BC=
如图,已知直三棱柱ABC-A1B1C1,侧棱长为2,底面△ABC中,∠B=90°,AB=1,BC=| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,BC=CC1=AC=a
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,BC=CC1=AC=a查看答案和解析>>
科目:高中数学 来源: 题型:
 (理科)如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,CC1>AC,∠ACB=90°,异面直线AC1与BA1所成角的大小为arccos
(理科)如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,CC1>AC,∠ACB=90°,异面直线AC1与BA1所成角的大小为arccos
| ||
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1=2
如图,在直三棱柱ABC-A1B1C1中,AC=BC=2,AB=AA1=2| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com