
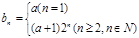 ;(2)
;(2)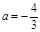 。
。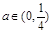 时,最小项为8a-1; 当
时,最小项为8a-1; 当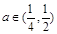 时,最小项为4a;当
时,最小项为4a;当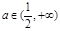 时,最小项为2a+1。 当
时,最小项为2a+1。 当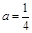 时,最小项为4a或8a-1当
时,最小项为4a或8a-1当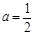 时,最小项为4a或2a+1;
时,最小项为4a或2a+1; 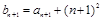 ,化简成与bn的代数式;
,化简成与bn的代数式;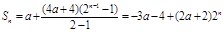 是等比数列,∴3a+4=0;
是等比数列,∴3a+4=0;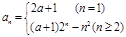 分类讨论,an单调性
分类讨论,an单调性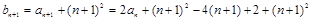
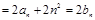 (n≥2)
(n≥2) 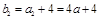 ,∵
,∵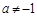 ,
,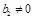 ,即
,即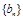 从第2项起是以2为公比的等比数列
从第2项起是以2为公比的等比数列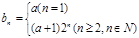
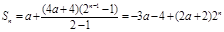 ∵
∵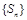 是等比数列, ∴3a+4=0,即
是等比数列, ∴3a+4=0,即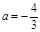 。
。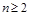 时,
时,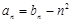 ,所以
,所以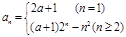 ,
,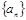 为2a+1,4a,8a-1,16a,32a+7,显然最小项是前三项中的一项。
为2a+1,4a,8a-1,16a,32a+7,显然最小项是前三项中的一项。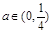 时,最小项为8a-1; 当
时,最小项为8a-1; 当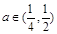 时,最小项为4a;当
时,最小项为4a;当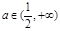 时,最小项为2a+1。
时,最小项为2a+1。 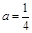 时,最小项为4a或8a-1当
时,最小项为4a或8a-1当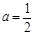 时,最小项为4a或2a+1;
时,最小项为4a或2a+1;

 巧学巧练系列答案
巧学巧练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com