
【题目】下列命题中正确的是( )
A.非零向量![]() 满足
满足![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为![]()
B.若![]() ,则
,则![]() 的夹角为锐角
的夹角为锐角
C.若![]() ,则
,则![]() 一定是直角三角形
一定是直角三角形
D.![]() 的外接圆的圆心为O,半径为1,若
的外接圆的圆心为O,半径为1,若![]() ,且
,且![]() ,则向量
,则向量![]() 在向量
在向量![]() 方向上的投影的数量为
方向上的投影的数量为![]()
【答案】ACD
【解析】
由平面向量的加、减法以及向量的夹角可判断A;利用向量的数量积的定义即可判断B;利用向量减法的几何意义以及向量的数量积即可判断C;根据题意可得三角形AOC为等边三角形,再根据向量数量积的几何意义即可求解.
对于A,由向量减法法则及题意知,向量![]() ,
,![]() 可以组成一个等边三角形,
可以组成一个等边三角形,
向量![]() 的夹角为
的夹角为![]() ,又由向量加法的平行四边形法则知,
,又由向量加法的平行四边形法则知,
以![]() 为邻边的平行四边形为菱形,所以
为邻边的平行四边形为菱形,所以![]() 与
与![]() 的夹角为
的夹角为![]() ,故选项A中说法正确;
,故选项A中说法正确;
对于B,当![]() 时,且同向时不成立,故选项B中说法错误;
时,且同向时不成立,故选项B中说法错误;
对于C,因为![]() ,
,
所以![]()
![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 是直角三角形,故选项C中说法正确;
是直角三角形,故选项C中说法正确;
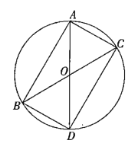
对于D,作图如下,其中四边形ABCD为平行四边形,因为![]() ,
,
所以O为AD、BC的交点,又![]() ,所以三角形AOC为等边三角形,
,所以三角形AOC为等边三角形,
所以![]() ,且BC为外接圆的直径,所以
,且BC为外接圆的直径,所以![]() .在直角三角形ABC中,
.在直角三角形ABC中,![]() ,
,![]() ,所以
,所以![]() ,则向量
,则向量![]() 在向量
在向量![]() 方向上的投影的数量为
方向上的投影的数量为
![]() .故选项D中说法正确.
.故选项D中说法正确.
故选:ACD.


科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,给定下列命题:
,给定下列命题:
①若方程![]() 有两个不同的实数根,则
有两个不同的实数根,则![]() ;
;
②若方程![]() 恰好只有一个实数根,则
恰好只有一个实数根,则![]() ;
;
③若![]() ,总有
,总有![]() 恒成立,则
恒成立,则![]() ;
;
④若函数![]() 有两个极值点,则实数
有两个极值点,则实数![]() .
.
则正确命题的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() :
:![]() 的右焦点,椭圆
的右焦点,椭圆![]() 上任意一点
上任意一点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到直线
到直线![]() :
:![]()
的距离之比为![]() 。
。
(1)求直线![]() 方程;
方程;
(2)设![]() 为椭圆
为椭圆![]() 的左顶点,过点
的左顶点,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 、
、![]() 两点,直线
两点,直线![]() 、
、![]() 与直线
与直线![]() 分别相交于
分别相交于![]() 、
、![]() 两点,以
两点,以![]() 为直径的圆是否恒过一定点?若是,求出定点坐标;若不是,请说明理由。
为直径的圆是否恒过一定点?若是,求出定点坐标;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知点P是![]() 所在平面外一点,M,N,K分别AB,PC,PA的中点,平面
所在平面外一点,M,N,K分别AB,PC,PA的中点,平面![]() 平面
平面![]() .
.

(1)求证:![]() 平面PAD;
平面PAD;
(2)直线PB上是否存在点H,使得平面![]() 平面ABCD,并加以证明;
平面ABCD,并加以证明;
(3)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式![]() >2010的n的最小值.
>2010的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花店每天以每枝![]() 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝![]() 元价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进![]() 枝玫瑰花,求当天的利润
枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝, ![]() )的函数解析式;
)的函数解析式;
(2)花店记录了![]() 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以![]() 天的各需求量的频率作为各需求量发生的概率.
天的各需求量的频率作为各需求量发生的概率.
![]() 若花店一天购进
若花店一天购进![]() 枝玫瑰花,
枝玫瑰花, ![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列, 数学期望及方差;
的分布列, 数学期望及方差;
![]() 若花店一天购进
若花店一天购进![]() 枝或
枝或![]() 枝玫瑰花,你认为应购进
枝玫瑰花,你认为应购进![]() 枝还是
枝还是![]() 枝?请说明理由.
枝?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形ABEF中,![]() ,
,![]() ,矩形ABEF可沿AB任意翻折.
,矩形ABEF可沿AB任意翻折.

(1)求证:当点F,A,D不共线时,线段MN总平行于平面ADF.
(2)“不管怎样翻折矩形ABEF,线段MN总与线段FD平行”这个结论正确吗?如果正确,请证明;如果不正确,请说明能否改变个别已知条件使上述结论成立,并给出理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com