练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    为了解某班学生喜爱打篮球是否与性别有关，对本班人进行了问卷调查得到了如下的列联表：

     
         		喜爱打篮球
         		不喜爱打篮球
         		合计
     
    男生
         		 
         		5
         		 
     
    女生
         		10
         		 
         		 
     
    合计
         		 
         		 
         		50
     
     
    已知在全部人中随机抽取1人抽到喜爱打篮球的学生的概率为．
    （1）请将上面的列联表补充完整(不用写计算过程)；
    （2）能否认为喜爱打篮球与性别有关？说明你的理由.(参考公式：，其中)

    （1）列联表如下：

     
    		喜爱打篮球
    		不喜爱打篮球
    		合计
    男生
    		20
    		5
    		25
    女生
    		10
    		15
    		25
    合计
    		30
    		20
    		50
     
    （2）有99%的把握认为喜爱打篮球与性别有关.

    解析试题分析：(1)根据在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率，求出喜爱打篮球的人数，进而求出男生的人数，填好表格；(2)根据所给的公式，代入数据求出观测值，把求得的结果与临界值进行比较，看出有多大的把握说明打篮球和性别有关系.
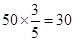    (1) 因为在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为，所以喜爱打篮球的总人数为人，所以列联表补充如下：

     
    		喜爱打篮球
    		不喜爱打篮球
    		合计
    男生
    		20
    		5
    		25
    女生
    		10
    		15
    		25
    合计
    		30
    		20
    		50
                            4分
    （2）根据列联表可得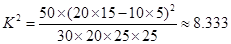
    因为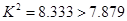            10分
    ∴有99%以上的把握认为喜爱打篮球与性别有关            12分.
    考点：独立性检验.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    某学校准备参加市运动会，对本校甲、乙两个田径队中30名跳高运动员进行了测试，并用茎叶图表示出本次测试30人的跳高成绩（单位cm），跳高成绩在175cm以上（包括175cm）定义为“合格”，成绩在175以下（不包括175cm）定义为“不合格”
    （1）求甲队队员跳高成绩的中位数
    （2）如果用分层抽样的方法从甲、乙两队所有的运动员中共抽取5人，则5人中“合格”与“不合格”的人数各为多少？
    （3）从甲队178cm以上（包括178cm）选取2人，至少有一人在186cm以上（包括186cm）的概率为多少？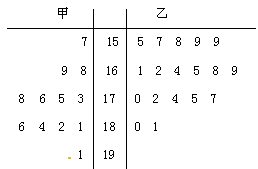

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某地区2007年至2013年农村居民家庭纯收入y（单位：千元）的数据如下表：

    年份
    		2007
    		2008
    		2009
    		2010
    		2011
    		2012
    		2013
    年份代号t
    		1
    		2
    		3
    		4
    		5
    		6
    		7
    人均纯收入y
    		2.9
    		3.3
    		3.6
    		4.4
    		4.8
    		5.2
    		5.9
     
    （1）求y关于t的线性回归方程；
    （2）利用（1）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.
    附：回归直线的斜率和截距的最小二乘法估计公式分别为：
    ，

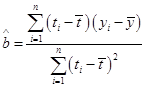    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某中学的数学测试中设置了“数学与逻辑”和“阅读与表达”两个内容，成绩分为A、B、C、D、E五个等级。某班考生两科的考试成绩的数据统计如图所示，其中“数学与逻辑”科目的成绩等级为B的考生有10人  
    （1）求该班考生中“阅读与表达”科目中成绩等级为A的人数；
    （2）若等级A、B、C、D、E分别对应5分、4分、3分、2分、1分，该考场共10人得分大于7分，其中2人10分，2人9分，6人8分，从这10人中随机抽取2人，求2人成绩之和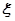的分布列。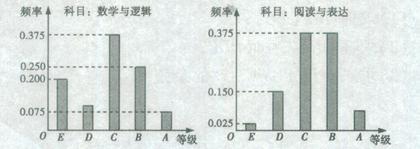

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    电视传媒为了解某市100万观众对足球节目的收视情况，随机抽取了100名观众进行调查．如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图，将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”， 并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”．
    （1）试估算该市“足球迷”的人数，并指出其中“铁杆足球迷”约为多少人；
    （2）该市要举办一场足球比赛，已知该市的足球场可容纳10万名观众．根据调查，如果票价定为100元/张，则非“足球迷”均不会到现场观看，而“足球迷”均愿意前往现场观看．如果票价提高元/张，则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少，“铁杆足球迷”愿意前往观看的人数会减少．问票价至少定为多少元/张时，才能使前往现场观看足球比赛的人数不超过10万人？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    以下是某地搜集到的新房屋的销售价格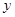（万元）和房屋的面积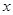（）的数据 ，若由资料可知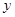对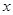呈线性相关关系。

    试求:（1）线性回归方程；
    （2）根据（1）的结果估计当房屋面积为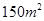时的销售价格.
    参考公式：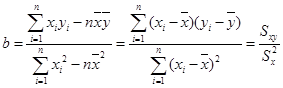

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某网站针对“2014年法定节假日调休安排”展开的问卷调查，提出了A、B、C三种放假方案，调查结果如下：

     
    		支持A方案
    		支持B方案
    		支持C方案
    35岁以下
    		200
    		400
    		800
    35岁以上（含35岁）
    		100
    		100
    		400
     
    （1）在所有参与调查的人中，用分层抽样的方法抽取n个人，已知从“支持A方案”的人中抽取了6人，求n的值；
    （2）在“支持B方案”的人中，用分层抽样的方法抽取5人看作一个总体，从这5人中任意选取2人，求恰好有1人在35岁以上（含35岁）的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某校研究性学习小组从汽车市场上随机抽取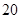辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于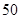公里和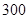公里之间，将统计结果分
    成组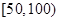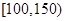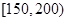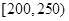：，，，，，绘制成如图所示的频率分布直方图．

    （1）求直方图中的值；
    （2）求续驶里程在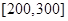的车辆数；
    （3）若从续驶里程在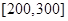的车辆中随机抽取2辆车，求其中恰有一辆车的续驶里程为 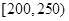的概率.

    查看答案和解析>>

    同步练习册答案