
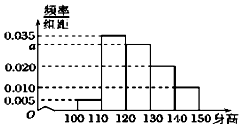
 从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).
从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).分析 (1)根据频率直方图的矩形面积之和为1,即可求a.
(2)根据众数、中位数、平均数的定义,结合频率分布直方图进行估计即可.
解答 解:(1)由直方图得(0.005+0.035+a+0.02+0.01)×10=1,解得a=0.03
(2)数值最多的数在(110,120),则估计众数=115;
第一组的频率为0.005×10=0.05,
第二组的频率为0.035×10=0.35,
第三组的频率为0.03×10=0.3,
则前两组的频率之和为0.05+0.35=0.4,
则中位数位于第三组(120,130),靠前的部分,估计中位数=123.3;
第四组的频率为0.02×10=0.2,
第五组的频率为0.01×10=0.1,
则平均数=105×0.05+115×0.35+125×0.3+135×0.2+145×0.1=124.5
点评 本题主要考查频率分布直方图的应用,以及众数、中位数、平均数的求解,考查学生的运算能力.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{3}{4}$x | B. | y=±$\frac{4}{3}$x | C. | y=±$\frac{3}{5}$x | D. | y=±$\frac{5}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若2x+1≥3,则x≥1 | B. | 若2x+1<3,则x<1 | C. | 若x≥1,则2x+1≥3 | D. | 若x<1,则2x+1≥3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com