
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
分析 求得双曲线的a,b,c,设|PF1|=m,|PF2|=n,由双曲线的定义,可得|m-n|=6,运用勾股定理,由S=$\frac{1}{2}$mn,即可求得△F1PF2的面积.
解答 解:由题意可得双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$的a=3,b=4,c=5,
左右焦点分别为F1(-5,0),F2(5,0),
设|PF1|=m,|PF2|=n,
由双曲线的定义可得|m-n|=6,
∠F1PF2=90°,
由勾股定理可得
100=m2+n2=(m-n)2+2mn=62+2mn,
∴mn=32.
则△F1PF2的面积S=$\frac{1}{2}$mn=$\frac{1}{2}$×32=16.
故选:B.
点评 本题主要考察了双曲线的定义、方程和简单性质,注意定义法和勾股定理,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | y=x2+|x| | B. | y=2x-2-x | C. | y=x2-3x | D. | y=$\frac{1}{x+1}$+$\frac{1}{x-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
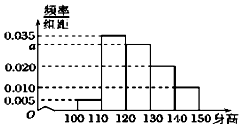 从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).
从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
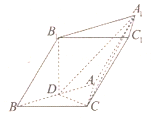 如图,在三棱柱ABC-A1B1C1中,D为AB的中点,CD⊥DA1,AC⊥BC,∠ABB1=45°,AC=BC=BB1=2.
如图,在三棱柱ABC-A1B1C1中,D为AB的中点,CD⊥DA1,AC⊥BC,∠ABB1=45°,AC=BC=BB1=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?{x_0}∈R,{x_0}^2+5{x_0}=4$ | B. | ?x∈R,x2+5x≠4 | ||
| C. | $?{x_0}∈R,{x_0}^2+5{x_0}≠4$ | D. | 以上都不正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com