
分析 (1)由已知得:$e=\frac{{\sqrt{4+m}}}{{\sqrt{3}}}$,$k=\frac{{\sqrt{m}}}{{\sqrt{3}}}$,利用e≥$\sqrt{2}$k,m>0,即可求m的取值范围;
(2)求出q的等价结论,利用p是q的必要不充分条件,求a的取值范围.
解答 解:(1)由已知得:$e=\frac{{\sqrt{4+m}}}{{\sqrt{3}}}$,$k=\frac{{\sqrt{m}}}{{\sqrt{3}}}$,
∵$e≥\sqrt{2}k$,∴$\frac{{\sqrt{3+m}}}{{\sqrt{3}}}≥\sqrt{2}•\frac{{\sqrt{m}}}{{\sqrt{3}}}$,解得m≤3,
∵m>0,∴0<m≤3,即m的取值范围(0,3].
(2)∵m2-(2a+2)m+a(a+2)≤0,∴(m-a)(m-a-2)≤0,即a≤m≤a+2,
∵p是q的必要不充分条件,∴$\left\{\begin{array}{l}a>0\\ a+2≤3\end{array}\right.$
解得0<a≤1,即a的取值范围为(0,1].
点评 本题考查双曲线的方程与性质,考查充要条件,知识综合性强.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -4 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
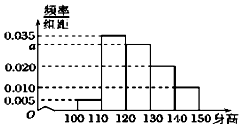 从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).
从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com