
【题目】“海水稻”就是耐盐碱水稻,是一种介于野生稻和栽培稻之间的普遍生长在海边滩涂地区,具有耐盐碱的水稻,它比其它普通的水稻均有更强的生存竞争能力,具有抗涝,抗病虫害,抗倒伏等特点,还具有预防和治疗多种疾病的功效,防癌效果尤为显著.海水稻的灌溉是将海水稀释后进行灌溉.某试验基地为了研究海水浓度![]() (‰)对亩产量
(‰)对亩产量![]() (吨)的影响,通过在试验田的种植实验,测得了某种海水稻的亩产量与海水浓度的数据如表.绘制散点图发现,可用线性回归模型拟合亩产量
(吨)的影响,通过在试验田的种植实验,测得了某种海水稻的亩产量与海水浓度的数据如表.绘制散点图发现,可用线性回归模型拟合亩产量![]() 与海水浓度
与海水浓度![]() 之间的相关关系,用最小二乘法计算得
之间的相关关系,用最小二乘法计算得![]() 与
与![]() 之间的线性回归方程为
之间的线性回归方程为![]() .
.
海水浓度 | 3 | 4 | 5 | 6 | 7 |
亩产量 | 0.62 | 0.58 | 0.49 | 0.4 | 0.31 |
残差 |
(1)请你估计:当浇灌海水浓度为8‰时,该品种的亩产量.
(2)①完成上述残差表:
②统计学中,常用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越大,模型拟合效果越好,并用它来说明预报变量与解释变量的相关性.你能否利用以上表格中的数据,利用统计学的相关知识,说明浇灌海水浓度对亩产量的贡献率?(计算中数据精确到
越大,模型拟合效果越好,并用它来说明预报变量与解释变量的相关性.你能否利用以上表格中的数据,利用统计学的相关知识,说明浇灌海水浓度对亩产量的贡献率?(计算中数据精确到![]() )
)
(附:残差公式![]() ,相关指数
,相关指数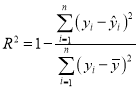 )
)
【答案】(1)当海水浓度为8‰时,该品种的亩产量为0.24吨(2)①填表见解析;②所以浇灌海水浓度对亩产量的贡献率是![]() ,详解见解析.
,详解见解析.
【解析】
(1)根据题意,算出![]() ,将样本中心点
,将样本中心点![]() 代入线性回归方程为
代入线性回归方程为![]() ,求出
,求出![]() ,从而可估计当浇灌海水浓度为8‰时,该品种的亩产量.
,从而可估计当浇灌海水浓度为8‰时,该品种的亩产量.
(2)根据线性回归方程![]() 和残差公式
和残差公式![]() ,即可求出个海水浓度时对应的残差,即可完成残差表;根据相关指数
,即可求出个海水浓度时对应的残差,即可完成残差表;根据相关指数![]() 的公式,求出
的公式,求出![]() ,根据
,根据![]() 的意义,即可得出浇灌海水浓度对亩产量的贡献率.
的意义,即可得出浇灌海水浓度对亩产量的贡献率.
(1)根据题意,可得![]() ,
,
![]() ,
,
而![]() 与
与![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,
,
则![]() ,解得:
,解得:![]() ,
,
当![]() 时,
时,![]() ,
,
所以当海水浓度为8‰时,该品种的亩产量为0.24吨.
(2)①由(1)知![]() ,
,
根据残差公式![]() ,得残差表如下:
,得残差表如下:
海水浓度 | 3 | 4 | 5 | 6 | 7 |
亩产量 | 0.62 | 0.58 | 0.49 | 0.4 | 0.31 |
残差 | -0.02 | 0.02 | 0.01 | 0 | -0.01 |
②根据题意,可得:
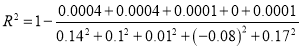
![]() ,
,
所以浇灌海水浓度对亩产量的贡献率是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为贯彻落实党中央全面建设小康社会的战略部署,某贫困地区的广大党员干部深入农村积极开展“精准扶贫”工作.经过多年的精心帮扶,截至2018年底,按照农村家庭人均年纯收入8000元的小康标准,该地区仅剩部分家庭尚未实现小康,2019年6月,为估计该地能否在2020年全面实现小康,统计了该地当时最贫困的一个家庭2019年1至6月的人均月纯收入,作出散点如下:
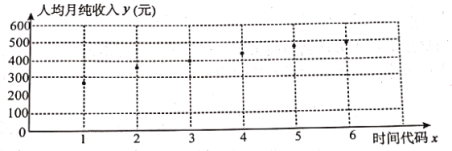
根据盯关性分析,发现其家庭人均月纯收入![]() 与时间代码
与时间代码![]() 之间具有较强的线性相关关系(记2019年1月、2月……分别为
之间具有较强的线性相关关系(记2019年1月、2月……分别为![]() ,
,![]() ,…,依此类推),由此估计该家庭2020年能实现小康生活.但2020年1月突如其来的新冠肺炎疫情影响了奔小康的进展,该家庭2020年第一季度每月的人均月纯收入只有2019年12月的预估值的
,…,依此类推),由此估计该家庭2020年能实现小康生活.但2020年1月突如其来的新冠肺炎疫情影响了奔小康的进展,该家庭2020年第一季度每月的人均月纯收入只有2019年12月的预估值的![]() .
.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)求该家庭2020年3月份的人均月纯收入;
(3)如果以该家庭3月份人均月纯收入为基数,以后每月增长率为![]() ,问该家庭2020年底能否实现小康生活?
,问该家庭2020年底能否实现小康生活?
参考数据:![]() ,
,![]() ,
,![]()
参考公式: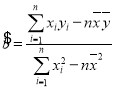 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年,新型冠状病毒引发的疫情牵动着亿万人的心,八方驰援战疫情,众志成城克时难,社会各界支援湖北共抗新型冠状病毒肺炎,重庆某医院派出3名医生,2名护士支援湖北,现从这5人中任选2人定点支援湖北某医院,则恰有1名医生和1名护士被选中的概率为( )
A.0.7B.0.4C.0.6D.0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数的简称,是一个反映居民家庭一般所购买的消费品和服务项目价格水平变动情况的宏观经济指标.同比一般情况下是今年第n月与去年第n月比;环比,表示连续2个统计周期(比如连续两月)内的量的变化比.如图是根据国家统计局发布的2019年4月—2020年4月我国CPI涨跌幅数据绘制的折线图,根据该折线图,则下列说法正确的是( )
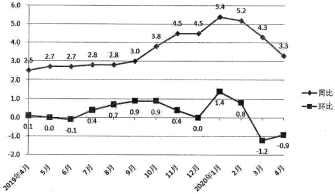
A.2020年1月CPI同比涨幅最大
B.2019年4月与同年12月相比较,4月CPI环比更大
C.2019年7月至12月,CPI一直增长
D.2020年1月至4月CPI只跌不涨
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的左右焦点分别为F1,F2点.M为椭圆上的一动点,△MF1F2面积的最大值为4.过点F2的直线l被椭圆截得的线段为PQ,当l⊥x轴时,
(a>b>0)的左右焦点分别为F1,F2点.M为椭圆上的一动点,△MF1F2面积的最大值为4.过点F2的直线l被椭圆截得的线段为PQ,当l⊥x轴时,![]() .
.
(1)求椭圆C的方程;
(2)过点F1作与x轴不重合的直线l,l与椭圆交于A,B两点,点A在直线![]() 上的投影N与点B的连线交x轴于D点,D点的横坐标x0是否为定值?若是,求出定值;若不是,请说明理由.
上的投影N与点B的连线交x轴于D点,D点的横坐标x0是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以直角坐标系的原点
为参数),在以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美团外卖和百度外卖两家公司其“骑手”的日工资方案如下:美团外卖规定底薪70元,每单抽成1元;百度外卖规定底薪100元,每日前45单无抽成,超出45单的部分每单抽成6元,假设同一公司的“骑手”一日送餐单数相同,现从两家公司个随机抽取一名“骑手”并记录其100天的送餐单数,得到如下条形图:
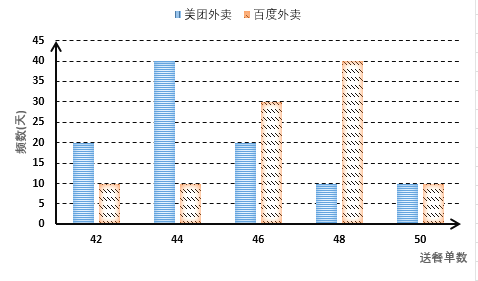
(Ⅰ)求百度外卖公司的“骑手”一日工资![]() (单位:元)与送餐单数
(单位:元)与送餐单数![]() 的函数关系;
的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
①记百度外卖的“骑手”日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小明拟到这两家公司中的一家应聘“骑手”的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新型冠状病毒疫情期间,商业活动受到很大影响某小型零售连锁店总部统计了本地区50家加盟店2月份的零售情况,统计数据如图所示.据估计,平均销售收入比去年同期下降40%,则去年2月份这50家加盟店的平均销售收入约为( )
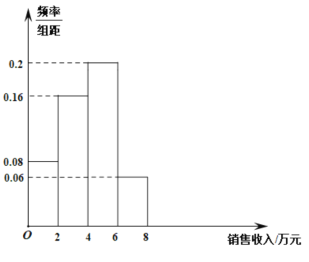
A.6.6万元B.3.96万元C.9.9万元D.7.92万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com