
| 3 |
| 8 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 8 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 27 |
| 8 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 6 |
| 3 |
| 2 |
| 5 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |


科目:高中数学 来源: 题型:
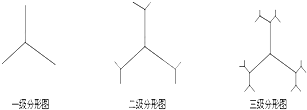 某种平面分形图如图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为120°;二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来
某种平面分形图如图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为120°;二级分形图是在一级分形图的每一条线段的末端再生成两条长度均为原来| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、[2,3] |
| B、[2,+∞) |
| C、(1.25,1.75) |
| D、(1.75,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com